
【题目】已知斜三棱柱![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
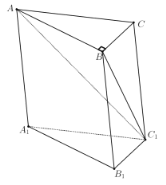
(1)求![]() 的长;
的长;
(2)求![]() 与面
与面![]() 所成的角的正切值.
所成的角的正切值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)方法一:由![]() ,
,![]() ,推出
,推出![]() 面
面![]() ,故
,故![]() ,则可利用勾股定理解出
,则可利用勾股定理解出![]() ;方法一:如图所示以
;方法一:如图所示以![]() 为原点,以
为原点,以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,竖直向上为
轴,竖直向上为![]() 轴,建立空间直角坐标系,因为
轴,建立空间直角坐标系,因为![]() 面
面![]() ,即
,即![]() 平面等同于
平面等同于![]() 平面,因而可以利用坐标求出
平面,因而可以利用坐标求出![]() ;
;
(2)方法一:延长![]() ,过
,过![]() 作
作![]() 于
于![]() ,因为
,因为![]() 面
面![]() ,所以面
,所以面![]() 面
面![]() ,所以
,所以![]() 面
面![]() ,所以
,所以![]() 为
为![]() 与面
与面![]() 所成角,等价于
所成角,等价于![]() 与面
与面![]() 所成的角,最后结合数据解三角形即可;方法二:建系后可以利用向量法求出
所成的角,最后结合数据解三角形即可;方法二:建系后可以利用向量法求出![]() 与面
与面![]() 所成的角的正切值.
所成的角的正切值.
解:方法一:(1)因为![]() ,
,![]() ,
,![]() ,
,
所以![]() 面
面![]() ,
,
故![]() ,所以
,所以![]() ,
,
于是![]() ;
;
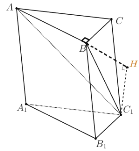
(2)延长![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
由(1)知![]() 面
面![]() ,所以面
,所以面![]() 面
面![]() ,
,
又面![]() 面
面![]() ,
,![]() ,
,![]() 面
面![]() ,
,
所以![]() 面
面![]() ,
,
所以![]() 为
为![]() 与面
与面![]() 所成角,
所成角,
在![]() 中可得
中可得![]() ,故
,故![]() ,
,![]() ,
,
所以![]() ,
,
又因为![]() ,面
,面![]() 面
面![]() ,
,
故![]() 与面
与面![]() 所成的角即为
所成的角即为![]() 与面
与面![]() 所成的角,
所成的角,
所以![]() 与面
与面![]() 所成的角的正切值为
所成的角的正切值为![]() .
.
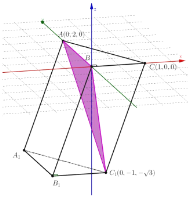
方法二:(1)如图所示以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,竖直向上为
轴,竖直向上为![]() 轴,
轴,
建立空间直角坐标系,则![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() 面
面![]() ,即
,即![]() 平面等同于
平面等同于![]() 平面,
平面,
又因为![]() ,
,![]() ,
,
所以![]() 的坐标为
的坐标为![]() ,
,
所以![]() ;
;
(2)因为![]() ,面
,面![]() 面
面![]() ,
,
故![]() 与面
与面![]() 所成的角即
所成的角即![]() 与面
与面![]() 所成的角,设其夹角为
所成的角,设其夹角为![]() ,
,
易得面![]() 的法向量为
的法向量为![]() ,且
,且![]() ,
,
所以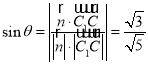 ,
,
所以![]() ,
,
所以![]() 与面
与面![]() 所成的角的正切值为
所成的角的正切值为![]() .
.


科目:高中数学 来源: 题型:
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为( )(注:![]() )
)
A.1624B.1024C.1198D.1560
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 是曲线
是曲线![]() 上任意一点,直线
上任意一点,直线![]() 与两坐标轴的交点分别为
与两坐标轴的交点分别为![]() ,求
,求![]() 最大值.
最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表给出的是某城市![]() 年至
年至![]() 年,人均存款
年,人均存款![]() (万元),人均消费
(万元),人均消费![]() (万元)的几组对照数据.
(万元)的几组对照数据.
年份 |
|
|
|
|
人均存款 |
|
|
|
|
人均消费 |
|
|
|
|
(1)试建立![]() 关于
关于![]() 的线性回归方程;如果该城市
的线性回归方程;如果该城市![]() 年的人均存款为
年的人均存款为![]() 万元,请根据线性回归方程预测
万元,请根据线性回归方程预测![]() 年该城市的人均消费;
年该城市的人均消费;
(2)计算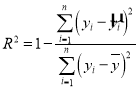 ,并说明线性回归方程的拟合效果.
,并说明线性回归方程的拟合效果.
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为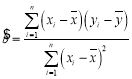 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x-1|+|x+m|.
(l)当m=l时,解不等式f(x)≥3;
(2)证明:对任意x∈R,2f(x)≥|m+1|-|m|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非常数列![]() 满足
满足![]() ,若
,若![]() ,则( )
,则( )
A.存在![]() ,
,![]() ,对任意
,对任意![]() ,
,![]() ,都有
,都有![]() 为等比数列
为等比数列
B.存在![]() ,
,![]() ,对任意
,对任意![]() ,
,![]() ,都有
,都有![]() 为等差数列
为等差数列
C.存在![]() ,
,![]() ,对任意
,对任意![]() ,
,![]() ,都有
,都有![]() 为等差数列
为等差数列
D.存在![]() ,
,![]() ,对任意
,对任意![]() ,
,![]() ,都有
,都有![]() 为等比数列
为等比数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com