
| 观看“导数的应用” 视频人数 | 观看“概率的应用” 视频人数 | 总计 | |
| A班 | |||
| B班 | |||
| 总计 |
| P(x2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
分析 (1)根据题目中的数据,完成2×2列联表,计算K2,对照数表即可得出结论;
(2)①利用分层抽样原理求出对应的数值;
②计算X的可能取值以及对应的概率值,列出X的分布列,求出数学期望值.
解答 解:(1)根据题目中的数据,完成下列2×2列联表:
| 观看“导数的应用” 视频人数 | 观看“概率的应用” 视频人数 | 总计 | |
| A班 | 40 | 20 | 60 |
| B班 | 25 | 35 | 60 |
| 总计 | 65 | 55 | 120 |
| X | 1 | 2 | 3 |
| P(X) | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查了独立性检验的应用问题,也考查了离散型随机变量的分布列与期望的应用问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3-cos1 | B. | 3+cos1 | C. | 1+cos1 | D. | 1-cos1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
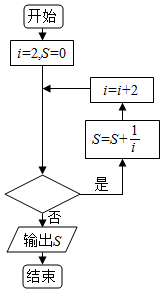
| A. | i≤4030? | B. | i≥4030? | C. | i≤4032? | D. | i≥4032? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象经过点(0,$\sqrt{3}$)和($\frac{2π}{9}$,0),则f($\frac{π}{2}$)的值为-1.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象经过点(0,$\sqrt{3}$)和($\frac{2π}{9}$,0),则f($\frac{π}{2}$)的值为-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com