
分析 (1)利用离心率为$\frac{\sqrt{2}}{2}$,中心O到直线AB的距离为$\frac{2}{\sqrt{3}}$.列出方程求出a,b,即可求解椭圆方程.
(2)设P(x,y),M(x1,y1),N(x2,y2),利用$\overrightarrow{OP}$=$λ\overrightarrow{OM}$+2μ$\overrightarrow{ON}$得,结合点P,M,N在椭圆上,
通过kQM•kQN=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$,得到λ2+4μ2=1,由椭圆的定义,推出|QF1|+|QF2|=2即可.
解答 解:(1)因为直线AB的方程为ax+by-ab=0.所以$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{2}{\sqrt{3}}$,
由已知得$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,故可解得a=2,b=$\sqrt{2}$;
所以椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$
(2)设P(x,y),M(x1,y1),N(x2,y2),
则由$\overrightarrow{OP}$=$λ\overrightarrow{OM}$+2μ$\overrightarrow{ON}$得,x=λx1+2μx2,y=λy1+2μy2
因为点P,M,N在椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$上,
所以x12+2y12=4,x22+2y22=4,x2+2y2=4
故x2+2y2=λ2(x12+2y12)+4μ2(x22+2y22)+4λμ(x1x2+2y1y2)=4λ2+16μ2+4λμ(x1x2+2y1y2)=4
设kQM,kQN分别为直线OM,ON的斜率,由题意知,kQM•kQN=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$,
因此x1•x2+2y1y2=0,所以λ2+4μ2=1,
λ2+$\frac{{μ}^{2}}{\frac{1}{4}}$=1,可知表达式是椭圆,a=1,b=$\frac{1}{2}$,c=$\frac{\sqrt{3}}{2}$,
而E1,E2恰为椭圆的左右焦点,
所以由椭圆的定义,|QF1|+|QF2|=2.
点评 本题考查椭圆的标准方程的求法,椭圆的简单性质的应用,直线与椭圆位置关系的应用,考查分析问题解决问题的能力,转化思想的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 观看“导数的应用” 视频人数 | 观看“概率的应用” 视频人数 | 总计 | |
| A班 | |||
| B班 | |||
| 总计 |
| P(x2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R | B. | [0,+∞) | C. | (0,+∞) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$i | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$i | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
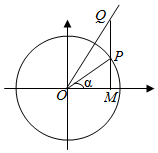 如图,在直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(-$\frac{π}{2}$,$\frac{π}{2}$).
如图,在直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(-$\frac{π}{2}$,$\frac{π}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com