Question

5．已知中心在坐标原点，焦点在x轴上的椭圆M的离心率为$\frac{1}{2}$，椭圆上异于长轴顶点的任意点A与左右两焦点F₁，F₂构成的三角形中面积的最大值为$\sqrt{3}$．
（Ⅰ）求椭圆M的标准方程；
（Ⅱ）若A与C是椭圆M上关于x轴对称的两点，连接CF₂与椭圆的另一交点为B，求证：直线AB与x轴交于定点．

Answer 1

分析 （Ⅰ）设椭圆M的标准方程为：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），由题意知：$\frac{c}{a}=\frac{1}{2}$，$\frac{1}{2}（2c）b=\sqrt{3}$，a²=b²+c²，联立解出即可得出．
（Ⅱ）设A（x₁，y₁），B（x₂，y₂），C（x₁，-y₁），AB：y=kx+m．代入$\frac{x^2}{4}+\frac{y^2}{3}=1$，可得（4k²+3）x²+8kmx+4m²-12=0．利用根与系数的关系、斜率计算公式可得m，k的关系式，即可得出．

解答 解：（Ⅰ）设椭圆M的标准方程为：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），
由题意知：$\frac{c}{a}=\frac{1}{2}$，$\frac{1}{2}（2c）b=\sqrt{3}$，a²=b²+c²，联立解得c=1，a=2，$b=\sqrt{3}$．
∴椭圆M的标准方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$．
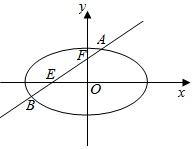
（Ⅱ）设A（x₁，y₁），B（x₂，y₂），C（x₁，-y₁），AB：y=kx+m．
将y=kx+m，代入$\frac{x^2}{4}+\frac{y^2}{3}=1$，可得（4k²+3）x²+8kmx+4m²-12=0．
则${x_1}+{x_2}=-\frac{8km}{{4{k^2}+3}}$，${x_1}{x_2}=\frac{{4{m^2}-12}}{{4{k^2}+3}}$．
∵B，C，F₂共线，∴${k_{B{F_2}}}={k_{C{F_2}}}$，即$\frac{{-（k{x_1}+m）}}{{{x_1}-1}}=\frac{{k{x_2}+m}}{{{x_2}-1}}$．
整理得2kx₁x₂+（m-k）（x₁+x₂）-2m=0，
∴$2k\frac{{4{m^2}-12}}{{4{k^2}+3}}-（m-k）\frac{8km}{{4{k^2}+3}}-2m=0$，m=-4k．
AB：y=k（x-4），与x轴交于定点P（4，0）．

点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、斜率计算公式、直线经过定点问题、三角形面积计算公式，考查了推理能力与计算能力，属于难题．