
 某校高三年级在一次质量考试中,考生成绩情况如表所示:
某校高三年级在一次质量考试中,考生成绩情况如表所示:| 成绩 累别 | [0,400) | [400,480) | [480,550) | [550,750) |
| 文科考生(人数) | 67 | 35 | 19 | z |
| 理科考生(人数) | 53 | x | y | 9 |
分析 (1)由分层抽样可得x,y,z的方程,解方程可得x,y,z值,即可求出次高三参加考试的总人数
(2)列举法可得总的基本事件共20种,符合条件的共4种,由古典概型的概率公式计算可得.
解答 解:(1)依题意$\frac{2}{z}$=$\frac{5-2}{9}$,∴z=6,
$\frac{19+6}{y+9}$=$\frac{1}{2}$,$\frac{35+19+6}{x+y+9}$=$\frac{2}{5}$ 解得x=100,y=41
所以本次高三参加考试的总人数为330人
(2)在这6名考生中随机抽取3名考生包含的基本事件为:
(121,130,135),(121,130,138),(121,130,142),(121,130,144),(121,135,138),
(121,135,142),(121,135,144),(121,138,142),(121,138,144),(121,142,144),(130,135,138),(130,135,142),(130,135,144),(130,138,142),(130,138,144),
(130,142,144),(135,138,142),(135,138,144),(135,142,144),(138,142,144)共20个,
其中“抽取的考生成绩均不低于13(5分)”包含的基本事件有4个,
其概率为$\frac{4}{20}$=$\frac{1}{5}$
点评 本题考查古典概型及其概率公式,涉及茎叶图和分层抽样,属基础题.


 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源: 题型:解答题
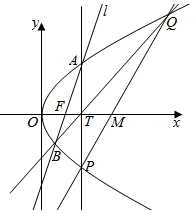 设抛物线C:y2=2px(p>0)的焦点为F,点T(t,0)(t>0),且过点F的直线,交C于A,B.
设抛物线C:y2=2px(p>0)的焦点为F,点T(t,0)(t>0),且过点F的直线,交C于A,B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
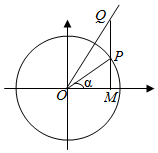 如图,在直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(-$\frac{π}{2}$,$\frac{π}{2}$).
如图,在直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(-$\frac{π}{2}$,$\frac{π}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com