
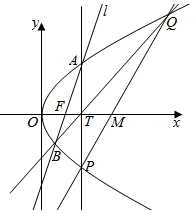
 设抛物线C:y2=2px(p>0)的焦点为F,点T(t,0)(t>0),且过点F的直线,交C于A,B.
设抛物线C:y2=2px(p>0)的焦点为F,点T(t,0)(t>0),且过点F的直线,交C于A,B.分析 (I)设过T的直线方程为x=my+t,代入y2=2px,利用韦达定理,结合两交点的纵坐标乘积为-4,t=2,求出p,即可求焦点F的坐标;
(Ⅱ)确定直线PQ的方程,令y=0可得x=-$\frac{{y}_{3}{y}_{4}}{2p}$=$\frac{2{t}^{2}}{p}$,证明|OF||OM|=|OT|2,即可得出结论.
解答 (I)解:设过T的直线方程为x=my+t,代入y2=2px,可得y2-2pmy-2pt=0,
由韦达定理可得,两根之积为-2pt,
∵两交点的纵坐标乘积为-4,
∴-2pt=4,
∵t=2,
∴p=1,
∴焦点F的坐标为($\frac{1}{2}$,0));
(Ⅱ)证明:设A(x1,y1),B(x2,y2),P(x3,y3),Q(x4,y4)
同理可得,y1y2=-p2,y1y3=-2pt,y2y4=-2pt,
∴y3y4=-4t2,
直线PQ的斜率为$\frac{{y}_{3}-{y}_{4}}{{x}_{3}-{x}_{4}}$=$\frac{2p}{{y}_{3}+{y}_{4}}$,
∴直线PQ的方程为y-y3=$\frac{2p}{{y}_{3}+{y}_{4}}$(x-x3).
令y=0可得x=-$\frac{{y}_{3}{y}_{4}}{2p}$=$\frac{2{t}^{2}}{p}$,
∴|OF||OM|=|OT|2,
∴|OF|,|OT|,|OM|成等比数列.
点评 本题考查直线与抛物线的位置关系,考查韦达定理的运用,考查等比数列的证明,考查学生分析解决问题的能力,属于中档题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0,1} | B. | {-3,-2,-1,0} | C. | {-2,-1,0} | D. | {-3,-2,-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | 9 | C. | $\frac{27}{2}$ | D. | $\frac{{9\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{y}^{2}}{3}$-$\frac{{x}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校高三年级在一次质量考试中,考生成绩情况如表所示:
某校高三年级在一次质量考试中,考生成绩情况如表所示:| 成绩 累别 | [0,400) | [400,480) | [480,550) | [550,750) |
| 文科考生(人数) | 67 | 35 | 19 | z |
| 理科考生(人数) | 53 | x | y | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com