
分析 (1)设M(x,y),由题意$\sqrt{{x}^{2}+(y-1)^{2}}$+|y-3|=4,分类讨论,可得点M的轨迹方程,并画出方程的曲线草图;
(2)若(x0,y0)∈C,则(-x0,y0)∈C,所以曲线C关于y轴对称,所以一定存在关于y轴对称的对称点,联立方程组,得到4y0=-12(2t-y0-4)化简得t=$\frac{{y}_{0}+6}{3}$,(0≤y0≤3),即可求出t的值.
解答 解:(1)设M(x,y),由题意$\sqrt{{x}^{2}+(y-1)^{2}}$+|y-3|=4,
①:当y≤3时,有$\sqrt{{x}^{2}+(y-1)^{2}}$=y+1,化简得:x2=4y
②:当y>3时,有$\sqrt{{x}^{2}+(y-1)^{2}}$=7-y,化简得:x2=-12(y-4)(二次函数)
综上所述:点M的轨迹方程为x2=$\left\{\begin{array}{l}{4y,y≤3}\\{-12(y-4),y>3}\end{array}\right.$(如图1),
(2)若(x0,y0)∈C,则(-x0,y0)∈C,所以曲线C关于y轴对称,所以一定存在关于y轴对称的对称点,
下面研究P(x0,y0)是轨迹x2=4y(y≤3)上任意一点,则x02=4y0,(y0≤3),它关于B(0,t)的对称点为Q(-x0,2t-y0),由于点Q在轨迹x2=-12(y-4)上,如图2.
所以(-x0)2=-12(2t-y0-4),联立方程组$\left\{\begin{array}{l}{{x}_{0}^{2}=4{y}_{0}^{\;}}\\{{x}_{0}^{2}=-12(2t-{y}_{0}-4)}\end{array}\right.$(*)得4y0=-12(2t-y0-4)化简得t=$\frac{{y}_{0}+6}{3}$,(0≤y0≤3),
当y0∈(0,3)时,t∈(2,3),此时方程组(*)有两解,即增加有两组对称点,
所以t的取值范围是(2,3)
点评 本题考查轨迹方程,考查点的对称性、一元二次方程根的判别式,考查学生分析解决问题的能力,难度大.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
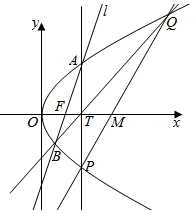 设抛物线C:y2=2px(p>0)的焦点为F,点T(t,0)(t>0),且过点F的直线,交C于A,B.
设抛物线C:y2=2px(p>0)的焦点为F,点T(t,0)(t>0),且过点F的直线,交C于A,B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
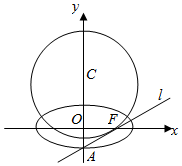 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的离心率e=$\frac{\sqrt{3}}{2}$,经过椭圆E的下顶点A和右焦点F的直线l的圆C:x2+(y-2b)2=$\frac{27}{4}$相切.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的离心率e=$\frac{\sqrt{3}}{2}$,经过椭圆E的下顶点A和右焦点F的直线l的圆C:x2+(y-2b)2=$\frac{27}{4}$相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com