
分析 (Ⅰ)法一:写出f(x)的分段函数的形式,求出f(x)的最小值,从而求出a的值即可;法二:根据绝对值的性质求出f(x)的最小值,从而求出a的值即可;
(Ⅱ)写出f(x)的分段函数的形式,通过讨论x的范围求出各个区间上的不等式的解集,取并集即可.
解答 解:(Ⅰ)解法1:∵a>0,
∴$f(x)=\left\{{\begin{array}{l}{-(a+2),\;(x<-2)}\\{2x+2-a,\;(-2≤x<a)}\\{a+2,\;(x≥a)}\end{array}}\right.$,--------------(2分)
当-2≤x<a时,-2-a≤f(x)<a+2,
∴当x∈R时,-2-a≤f(x)≤a+2---(4分)
∴f(x)min=-(a+2)=-3,∴a=1;--------------------------------------------------(5分)
解法2:∵||x+2|-|x-a||≤|(x+2)-(x-a)|=a+2,----------------------(2分)
∴|f(x)|≤a+2,f(x)min=-(a+2),---------------------------------------------(3分)
又已知f(x)min=-3,∴a=1;-----------------------------------(5分)】
(Ⅱ)由(Ⅰ)知$f(x)=\left\{{\begin{array}{l}{-(a+2),\;(x<-2)}\\{2x+2-a,\;(-2≤x<a)}\\{a+2,\;(x≥a)}\end{array}}\right.$,(a>0)
当x<-2时,f(x)=-(a+2)<-2,|f(x)|>2,不等式|f(x)|≤2解集为空集---(6分)
当x≥a时,f(x)=a+2>2,不等式|f(x)|≤2解集也为空集;----------------(7分)
当-2≤x<a时,|f(x)|≤2,即-2≤2x+2-a≤2⇒$\frac{a}{2}-2<x<\frac{a}{2}$
∵$\frac{a}{2}-2>-2$,$\frac{a}{2}<a$,∴当-2≤x<a时,|f(x)|≤2的解为$\frac{a}{2}-2<x<\frac{a}{2}$-----(9分)
综上得所求不等式的解集为$\{x|\frac{a}{2}-2<x<\frac{a}{2}\}$----------------------------(10分)
点评 本题考查了解绝对值不等式问题,考查分类讨论思想以及绝对值的性质,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{y}^{2}}{3}$-$\frac{{x}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
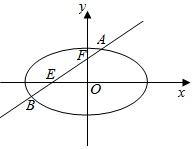 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长轴长为4,其上顶点到直线3x+4y-1=0的距离等于$\frac{3}{5}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长轴长为4,其上顶点到直线3x+4y-1=0的距离等于$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3-cos1 | B. | 3+cos1 | C. | 1+cos1 | D. | 1-cos1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com