
分析 设出Q的坐标,PQ的中点坐标,利用已知条件列出不等式,画出可行域,求解即可.
解答 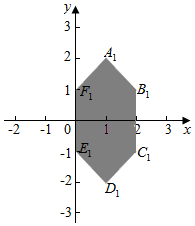 解:设线段PQ的中点(x,y),Q(m,n),P(2,t),t∈[-2,2].
解:设线段PQ的中点(x,y),Q(m,n),P(2,t),t∈[-2,2].
可得$\frac{m+2}{2}$=x,$\frac{n+t}{2}=y$,即m=2x-2,n=2y-t,
不等式|x|+|y|≤2表示的平面区域记为M,点Q是区域M上的动点,
可得:|2x-2|+|2y-t|≤2,t∈[-2,2].
即:|x-1|+|y-$\frac{t}{2}$|≤1,t∈[-2,2].
不等式表示的可行域如图:可得线段PQ的中点的运动区域的面积是一个长方形与两个等腰直角三角形的面积的和,即:2×2+2×$\frac{1}{2}$×2×1=6.
故答案为:6.
点评 本题考查线性规划的应用,转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
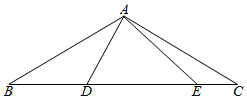 如图,在三角形ABC中,∠BAC=120°,AB=AC=2,D,E为BC边上的点,且$\overrightarrow{BC}$=3$\overrightarrow{BD}$=2$\overrightarrow{DE}$,则$\overrightarrow{AD}$•$\overrightarrow{AE}$=$\frac{1}{3}$.
如图,在三角形ABC中,∠BAC=120°,AB=AC=2,D,E为BC边上的点,且$\overrightarrow{BC}$=3$\overrightarrow{BD}$=2$\overrightarrow{DE}$,则$\overrightarrow{AD}$•$\overrightarrow{AE}$=$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
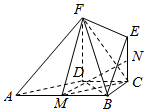 如图,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AB=4,EC∥FD,FD⊥底面ABCD,M是AB的中点.
如图,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AB=4,EC∥FD,FD⊥底面ABCD,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
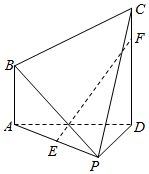 如图,四边形ABCD是直角梯形,AB∥CD,AB=$\frac{1}{2}$CD,AH⊥AD,平面ABCD⊥平面PAD,且△PAD为等边三角形,E是PA的中点,CF=$\frac{1}{4}$CD.
如图,四边形ABCD是直角梯形,AB∥CD,AB=$\frac{1}{2}$CD,AH⊥AD,平面ABCD⊥平面PAD,且△PAD为等边三角形,E是PA的中点,CF=$\frac{1}{4}$CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com