
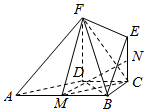
 如图,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AB=4,EC∥FD,FD⊥底面ABCD,M是AB的中点.
如图,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AB=4,EC∥FD,FD⊥底面ABCD,M是AB的中点.分析 (1)证明四边形BCDM是菱形,对角线BD⊥CM,再证明FD⊥CM,即可证明CM⊥平面BDF,从而得平面CFM⊥平面BDF;
(2)过点N作NP∥EF,交DF与点P,连接PM,证明平面PMN∥平面BEF,即可证明MN∥平面BEF.
解答 解:(1)证明:直角梯形ABCD中,AB∥CD,BC=2,AB=4,且M是AB的中点,
∴BM=CD,∴四边形BCDM是平行四边形,
又BC=CD=2,∴平行四边形BCDM是菱形;
∴BD⊥CM,
又FD⊥底面ABCD,CM?平面BCDM,∴FD⊥CM,
且FD∩BD=D,
∴CM⊥平面BDF,
有CM?平面CFM,
∴平面CFM⊥平面BDF;
(2)过点N作NP∥EF,交DF与点P,连接PM,如图所示;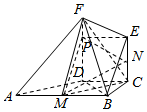
∵EC∥FD,∴四边形EFPN是平行四边形,
又点N为线段CE的中点,EC=2,FD=3,
∴FP=$\frac{1}{2}$EC=1,
PD=EC=2,
∴PE∥CD,且PE=CD,
又BM∥CD,且BM=CD,
∴BM∥PE,且PE=BM,
∴四边形BEPM为平行四边形,
∴PM∥BE;
又PM?平面BEF,BE?平面BEF,∴PM∥平面BEF;
同理,PM∥平面BEF,
又PM∩PN=P,PM?平面PMN,PN?平面PMN,
∴平面PMN∥平面BEF,
又MN?平面PMN,∴MN∥平面BEF.
点评 本题主要考查了线面平行,面面平行与垂直的应用问题,解题时应熟记空间中的平行关系与垂直关系的相互转化,是中档题目.求解


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:解答题
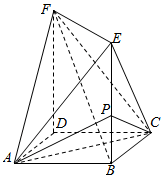 多面体ABCDEF中,底面ABCD为正方形,BE∥DF,BE=DF,BE⊥平面ABCD且 BE=2AB=2,点P是线段BE上的一点,且BP=λ.
多面体ABCDEF中,底面ABCD为正方形,BE∥DF,BE=DF,BE⊥平面ABCD且 BE=2AB=2,点P是线段BE上的一点,且BP=λ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{13}{2}$ | C. | 12 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | c<a<b | C. | a<b<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
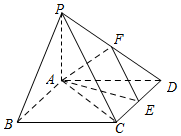 如图在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD中点,$\overrightarrow{CE}$=λ$\overrightarrow{CD}$(0<λ<1).
如图在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD中点,$\overrightarrow{CE}$=λ$\overrightarrow{CD}$(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com