
| A. | -3 | B. | -1 | C. | 0 | D. | 1 |
分析 由f(x)的解析式,可得f(-1)=1;f(3)=f(2)-f(1)=-f(0),再由第一段解析式,运用对数的运算性质即可得到所求和.
解答 解:由f(x)=$\left\{\begin{array}{l}{log}_{2}(1-x)(x≤0)\\ f(x-1)-f(x-2)(x>0)\end{array}$,可得:
f(-1)=log2[1-(-1)]=log22=1,
f(3)=f(2)-f(1)=f(1)-f(0)-f(1)=-f(0)
=-log21=0,
即有f(3)+f(-1)=0+1=1.
故选:D.
点评 本题考查分段函数的运用:求函数值,注意运用对应的解析式,考查运算能力,属于基础题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40、24 | B. | 40、36 | C. | 24、36 | D. | 24、40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x0∈R,2x0>0 | B. | 存在x0∈R,2x0≥0 | ||
| C. | 对任意的x∈R,2x≤0 | D. | 对任意的x∈R,2x>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:4 | B. | 2:3 | C. | 1:3 | D. | 1:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
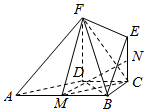 如图,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AB=4,EC∥FD,FD⊥底面ABCD,M是AB的中点.
如图,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AB=4,EC∥FD,FD⊥底面ABCD,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
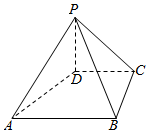 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com