
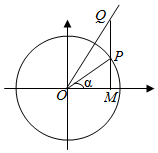
 如图,在直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(-$\frac{π}{2}$,$\frac{π}{2}$).
如图,在直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(-$\frac{π}{2}$,$\frac{π}{2}$).分析 ﹙Ⅰ﹚同角三角的基本关系求得cosα的值,再利用两角差的余弦公式求得cos∠POQ的值.
(Ⅱ)利用用割补法求三角形POQ的面积,再利用正弦函数的值域,求得它的最值.
解答 解:﹙Ⅰ﹚因为$sinα=\frac{1}{3}$,且$α∈(-\frac{π}{2},\frac{π}{2})$,所以$cosα=\frac{{2\sqrt{2}}}{3}$.
所以$cos∠POQ=cos(\frac{π}{3}-α)=cos\frac{π}{3}cosα+sin\frac{π}{3}sinα=\frac{{2\sqrt{2}+\sqrt{3}}}{6}$.
(Ⅱ)由三角函数定义,得P(cosα,sinα),从而$Q(cosα,\sqrt{3}cosα)$,
所以 ${S_{△POQ}}=\frac{1}{2}|cosα||\sqrt{3}cosα-sinα|$=$\frac{1}{2}|\sqrt{3}{cos^2}α-sinαcosα|$=$\frac{1}{2}|\frac{{\sqrt{3}}}{2}+\frac{{\sqrt{3}cos2α}}{2}-\frac{1}{2}sin2α|=\frac{1}{2}|\frac{{\sqrt{3}}}{2}+sin(\frac{π}{3}-2α)|$
$≤\frac{1}{2}|\frac{{\sqrt{3}}}{2}+1|=\frac{{\sqrt{3}}}{4}+\frac{1}{2}$.
因为$α∈(-\frac{π}{2},\frac{π}{2})$,所以当$α=-\frac{π}{12}$时,等号成立,
所以△OPQ面积的最大值为$\frac{{\sqrt{3}}}{4}+\frac{1}{2}$.
点评 本题主要考查任意角三角函数的定义,正弦函数的值域,用割补法求三角形的面积,属于中档题.


科目:高中数学 来源: 题型:解答题
 某校高三年级在一次质量考试中,考生成绩情况如表所示:
某校高三年级在一次质量考试中,考生成绩情况如表所示:| 成绩 累别 | [0,400) | [400,480) | [480,550) | [550,750) |
| 文科考生(人数) | 67 | 35 | 19 | z |
| 理科考生(人数) | 53 | x | y | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | 人数(人) |
| 19 | 7 |
| 21 | 2 |
| 28 | 3 |
| 30 | 4 |
| 31 | 5 |
| 32 | 3 |
| 40 | 6 |
| 合计 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂对某产品的产量与单位成本的资料分析后有如表数据:
某工厂对某产品的产量与单位成本的资料分析后有如表数据:| 月 份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 产量x千件 | 2 | 3 | 4 | 3 | 4 | 5 |
| 单位成本y元/件 | 73 | 72 | 71 | 73 | 69 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{2}$,2) | B. | [-$\sqrt{2}$,1) | C. | ($\sqrt{2}$,2) | D. | (-$\sqrt{2}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$sin(B+$\frac{π}{3}$) | B. | 6sin(B+$\frac{π}{3}$) | C. | 4$\sqrt{3}$sin(B+$\frac{π}{6}$) | D. | 6sin(B+$\frac{π}{6}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com