
 某工厂对某产品的产量与单位成本的资料分析后有如表数据:
某工厂对某产品的产量与单位成本的资料分析后有如表数据:| 月 份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 产量x千件 | 2 | 3 | 4 | 3 | 4 | 5 |
| 单位成本y元/件 | 73 | 72 | 71 | 73 | 69 | 68 |
分析 (Ⅰ) 根据所给的六组数据写出六个有序数对,在平面直角坐标系上点出对应的点,得到散点图,观察散点图呈带状分布,知产量与单位成本是线性相关.
(II)做出横标和纵标的平均数,得到这组数据的样本中心点,求出利用最小二乘法所需要的数据,代入关于b的公式,求出线性回归方程的系数,再求出a的值,得到方程.
解答 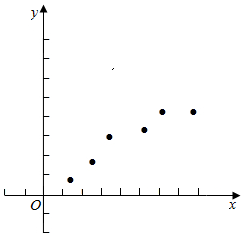 解:(Ⅰ) 根据所给的六组数据写出六个有序数对,在平面直角坐标系上点出对应的点,得到散点图,
解:(Ⅰ) 根据所给的六组数据写出六个有序数对,在平面直角坐标系上点出对应的点,得到散点图,
观察散点图呈带状分布,知产量与单位成本是线性相关;
(Ⅱ) 已计算得:x1y1+x2y2+…+x6y6=1481,$\overline x=\frac{21}{6},\overline y=71,\sum_{i=1}^6{x_i^2}=79,\sum_{i=1}^6{{x_i}{y_i}}=1481$,
代入公式得:$b=\frac{{1481-6×\frac{21}{6}×71}}{{79-6×{{({\frac{21}{6}})}^2}}}≈-1.82,a=71-({-1.82})×\frac{21}{6}≈77.37$
故线性回归方程为:y=77.37-1.82x.
点评 本题考查线性回归方程的求解,本题解题的关键是正确求解线性回归方程的系数,这里的运算比较麻烦,容易出错.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R | B. | [0,+∞) | C. | (0,+∞) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
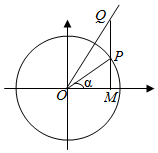 如图,在直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(-$\frac{π}{2}$,$\frac{π}{2}$).
如图,在直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(-$\frac{π}{2}$,$\frac{π}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
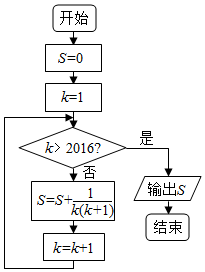
| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2017}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com