练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．执行如图所示的程序框图，则输出的结果是（　　）
    A．$\frac{2014}{2015}$B．$\frac{2015}{2016}$C．$\frac{2016}{2017}$D．$\frac{2017}{2018}$

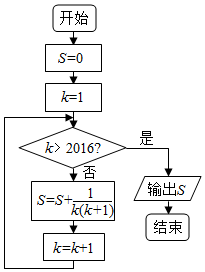
    分析 根据框图的流程模拟运行程序，直到不满足条件，计算输出S的值．

    解答 解：k=1＜2016，s=$\frac{1}{2}$，
    k=2＜2016，s=$\frac{1}{2}$+$\frac{1}{6}$=$\frac{2}{3}$，
    k=3＜2016，s=$\frac{2}{3}$+$\frac{1}{12}$=$\frac{3}{4}$，
    …，
    k=2015＜2016，s=$\frac{2015}{2016}$，
    k=2016=2016，s=$\frac{2016}{2017}$，
    输出s，
    故选：C．

    点评 本题考查了循环结构的程序框图，根据框图的流程模拟运行程序是解答此类问题的常用方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．已知正项数列{an}的前n项和为Sn，若4S${\;}_{n}^{2}$-2=a${\;}_{n}^{2}$+$\frac{1}{{a}_{n}^{2}}$（n∈N*），则S400=20．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．某工厂对某产品的产量与单位成本的资料分析后有如表数据：
    月     份12345
    6
    产量x千件234345
    单位成本y元/件737271736968
    （Ⅰ） 画出散点图，并判断产量与单位成本是否线性相关．
    （Ⅱ） 求单位成本y与月产量x之间的线性回归方程．（其中结果保留两位小数）
    参考公式：用最小二乘法求线性回归方程系数公式：$\widehatb$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_1^2-n{{\overline x}^2}}}}$，$\widehata$=$\overline y$-$\widehatb\overline x$．
    （附：线性回归方程$\widehaty$=$\widehatb$x+$\widehata$中，b=$\frac{{\sum_{i=1}^n{（{x_i}-\overline x）}（{y_i}-\overline y）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$\widehata$=$\overline y$-$\widehatb\overline x$，其中$\overline{x}$，$\overline{y}$为样本平均值，$\hat b，\hat a$的值的结果保留二位小数．）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知向量$\overrightarrow{a}$=（cosα-1，sinα+3）（α∈R），$\overrightarrow{b}$=（4，1），则|$\overrightarrow{a}$+$\overrightarrow{b}$|的最大值为（　　）
    A．4B．5C．6D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知集合A={x|1＜x＜2}，B={x|x2≥2}，则∁R（A∪B）等于（　　）
    A．（-$\sqrt{2}$，2）B．[-$\sqrt{2}$，1）C．（$\sqrt{2}$，2）D．（-$\sqrt{2}$，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．某居民小区有两个相互独立的安全防范系统A和B，系统A和系统B在任意时刻发生故障的概率分别为$\frac{1}{8}$和p．若在任意时刻恰有一个系统不发生故障的概率为$\frac{9}{40}$，则p=（　　）
    A．$\frac{1}{10}$B．$\frac{2}{15}$C．$\frac{1}{6}$D．$\frac{1}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知点P（-1，2），线段PQ的中点M的坐标为（1，-1）．若向量$\overrightarrow{PQ}$与向量a=（λ，1）共线，则λ=-$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知抛物线y2=8x的准线与双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{16}$=1相交于A，B两点，如果抛物线的焦点F总在以AB为直径的圆的内部，则双曲线的离心率取值范围是（　　）
    A．（3，+∞）B．（1，3）C．（2，+∞）D．（1，$\sqrt{3}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知fn（x）=$\sum_{k=0}^{n}$C${\;}_{n}^{k}$xk（n∈N*）．
    （1）若g（x）=f4（x）+2f5（x）+3f6（x），求g（x）中含x4项的系数；
    （2）证明：C${\;}_{m+1}^{0}$+2C${\;}_{m+2}^{1}$+3C${\;}_{m+3}^{2}$+…+nC${\;}_{m+n}^{n-1}$=[$\frac{（m+2）n+1}{m+3}$]C${\;}_{m+n+1}^{m+2}$．

    查看答案和解析>>

    同步练习册答案