
| A. | (3,+∞) | B. | (1,3) | C. | (2,+∞) | D. | (1,$\sqrt{3}$) |
分析 先根据抛物线方程求得准线方程,代入双曲线方程求得y,根据抛物线的焦点F总在以AB为直径的圆的内部得到$\frac{4}{a}$$\sqrt{4-{a}^{2}}$>4,求出a的范围,利用a,b和c的关系求得c,则双曲线的离心率范围可得.
解答 解:抛物线y2=8x,则其准线方程为x=-2,焦点f(2,0),
∴焦点到准线的距离为p=4,
将准线方程为x=-2代入双曲线方程得y=±$\frac{4}{a}$$\sqrt{4-{a}^{2}}$,
∴以AB为直径的圆的半径为r=$\frac{4}{a}$$\sqrt{4-{a}^{2}}$,
∵抛物线的焦点F总在以AB为直径的圆的内部,
∴$\frac{4}{a}$$\sqrt{4-{a}^{2}}$>4,
∴$\left\{\begin{array}{l}{4-{a}^{2}≥0}\\{4-{a}^{2}>{a}^{2}}\end{array}\right.$,
解得0<a<$\sqrt{2}$
∴e=$\frac{c}{a}$=$\frac{\sqrt{16+{a}^{2}}}{a}$=$\sqrt{\frac{16}{{a}^{2}}+1}$>$\sqrt{\frac{16}{2}+1}$=3,
∴e>3,
故选:A.
点评 本题主要考查了抛物线和双曲线的简单性质.解题的关键是通过其性质求出a的范围,属于中档题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
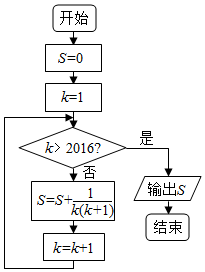
| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2017}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com