
分析 (1)利用fn(x)=(1+x)n,即可求出g(x)中含x4项的系数;
(2)令h(x)=(1+x)m+1+2(1+x)m+2+3(1+x)m+3+…+n•(1+x)m+n,利用错位相减法,即可证明结论.
解答 (1)解:fn(x)=$\sum_{k=0}^{n}$C${\;}_{n}^{k}$xk(n∈N*)=${C}_{n}^{0}$•x0+${C}_{n}^{1}$•x+${C}_{n}^{2}$•x2+${C}_{n}^{n}$•xn=(1+x)n,
g(x)=f4(x)+2f5(x)+3f6(x)=(1+x)4+2(1+x)5+3(1+x)6,
故g(x)中含x4项的系数为${C}_{4}^{4}$+2${C}_{5}^{4}$+3${C}_{6}^{4}$=56.
(2)证明:∵C${\;}_{m+1}^{0}$+2C${\;}_{m+2}^{1}$+3C${\;}_{m+3}^{2}$+…+nC${\;}_{m+n}^{n-1}$=${C}_{m+1}^{m+1}$+2${C}_{m+2}^{m+1}$+3${C}_{m+3}^{m+1}$+…+n${C}_{m+n}^{m+1}$,
令h(x)=(1+x)m+1+2(1+x)m+2+3(1+x)m+3+…+n•(1+x)m+n.
则函数h(x)中含xm+1项的系数为 C${\;}_{m+1}^{0}$+2C${\;}_{m+2}^{1}$+3C${\;}_{m+3}^{2}$+…+n${C}_{m+n}^{m+1}$,…(5分)
同乘1+x,由错位相减法得:-xh(x)=(1+x)m+1+(1+x)m+2+(1+x)m+3+…+(1+x)m+n-n•(1+x)m+n+1=$\frac{(1+x)^{m+1}[1-(1+x)^{n}]}{1-(1+x)}$-n•(1+x)m+n+1,
∴x2h(x)=(1+x)m+1-(1+x)m+n+1+n•(1+x)m+n+1,
h(x)中含xm+1项的系数,即是等式左边含xm+3项的系数,等式右边含xm+3项的系数为-${C}_{m+n+1}^{m+3}$+n${C}_{m+n+1}^{m+2}$,…(7分)
-${C}_{m+n+1}^{m+3}$+n${C}_{m+n+1}^{m+2}$=-$\frac{(m+n+1)!}{(m+3)!(n-2)!}$+n${C}_{m+n+1}^{m+2}$=-$\frac{n-1}{m+3}$${C}_{m+n+1}^{m+2}$+n${C}_{m+n+1}^{m+2}$=[$\frac{(m+2)n+1}{m+3}$]C${\;}_{m+n+1}^{m+2}$,
所以C${\;}_{m+1}^{0}$+2C${\;}_{m+2}^{1}$+3C${\;}_{m+3}^{2}$+…+nC${\;}_{m+n}^{n-1}$=[$\frac{(m+2)n+1}{m+3}$]C${\;}_{m+n+1}^{m+2}$. …(10分)
点评 本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
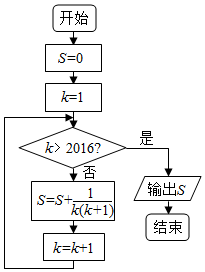
| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2017}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
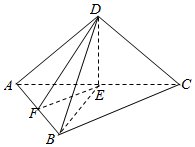 如图,在三棱锥D-ABC中,DA=DB=DC,D在底面ABC上的射影为E,AB⊥BC,DF⊥AB于F
如图,在三棱锥D-ABC中,DA=DB=DC,D在底面ABC上的射影为E,AB⊥BC,DF⊥AB于F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),其离心率与双曲线$\frac{x^2}{3}-{y^2}$=1的离心率互为倒数,而直线x+y=$\sqrt{3}$过椭圆C的一个焦点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),其离心率与双曲线$\frac{x^2}{3}-{y^2}$=1的离心率互为倒数,而直线x+y=$\sqrt{3}$过椭圆C的一个焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com