练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知△ABC中，a=1，b=2，C=$\frac{2π}{3}$，则边c的长度为$\sqrt{7}$．

    分析 直接利用余弦定理，列出方程求解即可．

    解答 解：△ABC中，a=1，b=2，C=$\frac{2π}{3}$，则边c=$\sqrt{{a}^{2}+{b}^{2}-2abcosC}$=$\sqrt{1+4+2×1×2×\frac{1}{2}}$=$\sqrt{7}$．
    故答案为：$\sqrt{7}$．

    点评 本题考查余弦定理的应用，三角形的解法，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．已知集合A={x|1＜x＜2}，B={x|x2≥2}，则∁R（A∪B）等于（　　）
    A．（-$\sqrt{2}$，2）B．[-$\sqrt{2}$，1）C．（$\sqrt{2}$，2）D．（-$\sqrt{2}$，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．在△ABC中，A=$\frac{π}{3}$，BC=3，则AB+AC的长可表示为（　　）
    A．4$\sqrt{3}$sin（B+$\frac{π}{3}$）B．6sin（B+$\frac{π}{3}$）C．4$\sqrt{3}$sin（B+$\frac{π}{6}$）D．6sin（B+$\frac{π}{6}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

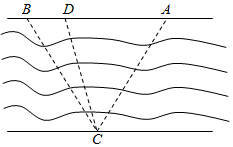    11．如图，江的两岸可近似的看成两平行的直线，江岸的一侧有A，B两个蔬菜基地，江的另一侧点C处有一个超市．已知A、B、C中任意两点间的距离为20千米．超市欲在AB之间建一个运输中转站D，A，B两处的蔬菜运抵D处后，再统一经过货轮运抵C处．由于A，B两处蔬菜的差异，这两处的运输费用也不同．如果从A处出发的运输费为每千米2元，从B处出发的运输费为每千米1元，货轮的运输费为每千米3元． 
    （1）设∠ADC=α，试将运输总费用S（单位：元）表示为α的函数S（α），并写出自变量的取值范围；
    （2）问中转站D建在何处时，运输总费用S最小？并求出最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．甲、乙、丙三人一起玩“黑白配”游戏：甲、乙、丙三人每次都随机出“手心（白）”、“手背（黑）”中的某一个手势，当其中一个人出示的手势与另外两人都不一样时，这个人胜出；其他情况，不分胜负．则一次游戏中甲胜出的概率是$\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知fn（x）=$\sum_{k=0}^{n}$C${\;}_{n}^{k}$xk（n∈N*）．
    （1）若g（x）=f4（x）+2f5（x）+3f6（x），求g（x）中含x4项的系数；
    （2）证明：C${\;}_{m+1}^{0}$+2C${\;}_{m+2}^{1}$+3C${\;}_{m+3}^{2}$+…+nC${\;}_{m+n}^{n-1}$=[$\frac{（m+2）n+1}{m+3}$]C${\;}_{m+n+1}^{m+2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=axex，曲线y=f（x）在点（0，f（0））处的切线方程为y=2x+b．
    （1）求实数a，b的值；
    （2）设函数g（x）=f（x）-x2-2x，求函数g（x）的单调区间；
    （3）在（2）的条件下，是否存在实数k，使得对于任意的x∈（-∞，0），都有g（x）≤kx恒成立？若存在，求出实数k的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知椭圆C的中心在原点，一个焦点为F（0，$\sqrt{3}$），且椭圆C经过点P（$\frac{1}{2}$，$\sqrt{3}$）．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）过点M（0，1）的斜率不为0的直线与椭圆交于A、B两点，A关于y轴的对称点为A′，求证：A′B恒过y轴上的一个定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知抛物线C：y2=16x，焦点为F，直线l：x=-1，点A∈l，线段AF与抛物线C的交点为B，若|FA|=5|FB|，则|FA|=（　　）
    A．$6\sqrt{2}$B．35C．$4\sqrt{3}$D．40

    查看答案和解析>>

    同步练习册答案