
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 由向量的坐标加法运算求得$\overrightarrow{a}$+$\overrightarrow{b}$的坐标,代入斜率模的公式,化简后利用辅助角公式化积得答案.
解答 解:∵$\overrightarrow{a}$=(cosα-1,sinα+3)(α∈R),$\overrightarrow{b}$=(4,1),
∴$\overrightarrow{a}+\overrightarrow{b}=(cosα+3,sinα+4)$,
则|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{(cosα+3)^{2}+(sinα+4)^{2}}$=$\sqrt{8sinα+6cosα+26}$
=$\sqrt{10sin(α+β)+26}$(tanβ=$\frac{3}{4}$).
当sin(α+β)=1时,$|\overrightarrow{a}+\overrightarrow{b}{|}_{max}=6$.
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|的最大值为6.
故选:C.
点评 本题考查平面向量的数量积运算,考查了同角三角函数基本关系式的应用,训练了三角函数最值的求法,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
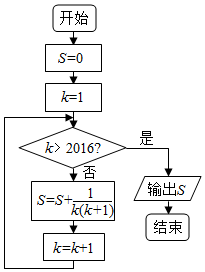
| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2017}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com