
将形如 的符号称二阶行列式,现规定
的符号称二阶行列式,现规定 , 函数
, 函数 =
= 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点,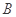 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形。
为正三角形。
(1)求 的值及函数
的值及函数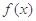 的单调递增区间;
的单调递增区间;
(2)若 ,在
,在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
已知向量 ,函数
,函数 ,且
,且 的图像过点
的图像过点 和点
和点 .
.
(1)求 的值;
的值;
(2)将 的图像向左平移
的图像向左平移 个单位后得到函数
个单位后得到函数 的图像,若
的图像,若 图像上各最高点到点
图像上各最高点到点 的距离的最小值为1,求
的距离的最小值为1,求 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=Asin(2x+θ),其中A≠0,θ∈(0, ).
).
(1)若函数f(x)的图象过点E(- ,1),F(
,1),F( ,
, ),求函数f(x)的解析式;
),求函数f(x)的解析式;
(2)如图,点M,N是函数y=f(x)的图象在y轴两侧与x轴的两个相邻交点,函数图象上一点P(t, )满足
)满足 ·
· =
= ,求函数f(x)的最大值.
,求函数f(x)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com