
| 1 |
| 2 |
| n |
| 2 |
| bn+1 |
| bn |
| (n+2)an+1-(n+1)+2 |
| (n+1)an-n+2 |
| ||||
| (n+1)an-n+2 |
| ||||
| (n+1)an-n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| n+1 |
| 1 |
| 2 |
| n-2 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| 2 |
| n-2 |
| n(n+1) |
| 1 |
| n+1 |
| 1 |
| 2 |
| n-2 |
| n(n+1) |
| 1 |
| n+1 |
| 1 |
| 2 |
| n-2 |
| n(n+1) |
| n-1 |
| (n+1)(n+2) |
| n-2 |
| n(n+1) |
| 4-n |
| n(n+1)(n+2) |
| 1 |
| 2 |
| n |
| 2 |
| bn+1 |
| bn |
| (n+2)an+1-(n+1)+2 |
| (n+1)an-n+2 |
| ||||
| (n+1)an-n+2 |
| ||||
| (n+1)an-n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| 2 |
| n-2 |
| n+1 |
| n |
| n+1 |
| 1 |
| 2 |
| n-2 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| 2 |
| n-2 |
| n(n+1) |
| 1 |
| n+1 |
| 1 |
| 2 |
| n-2 |
| n(n+1) |
| 1 |
| n+1 |
| 1 |
| 2 |
| n-2 |
| n(n+1) |
| n-1 |
| (n+1)(n+2) |
| n-2 |
| n(n+1) |
| 4-n |
| n(n+1)(n+2) |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 16 |
| 1 |
| 40 |
| 1 |
| 96 |
| 1 |
| 2 |
| 1 |
| 12 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 6 |
| 7 |
| 48 |
| 1 |
| 8 |
| 53 |
| 480 |
| 1 |
| 6 |
| 1 |
| 6 |


科目:高中数学 来源: 题型:
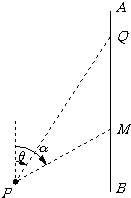 (2008•江苏二模)如图,AB是沿太湖南北方向道路,P为太湖中观光岛屿,Q为停车场,PQ=5.2km.某旅游团游览完岛屿后,乘游船回停车场Q,已知游船以13km/h的速度沿方位角θ的方向行驶,sinθ=
(2008•江苏二模)如图,AB是沿太湖南北方向道路,P为太湖中观光岛屿,Q为停车场,PQ=5.2km.某旅游团游览完岛屿后,乘游船回停车场Q,已知游船以13km/h的速度沿方位角θ的方向行驶,sinθ=| 5 |
| 13 |
| 4 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•江苏二模)如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0)(a>0).设△AOB和△COD的外接圆圆心分别为M,N.
(2008•江苏二模)如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0)(a>0).设△AOB和△COD的外接圆圆心分别为M,N.| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com