练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在双曲线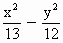＝－1的一支上有不同三点A，6)，C()与焦点F(0，5)的距离成等差数列，(1)求；(2)求证线段AC的垂直平分线经过某一定点，并求出定点的坐标．

    答案：
    解析：

    解:双曲线方程为，焦点坐标为(0，－5)，(0，5)，准线方程为y＝±．如图，设P()是双曲线＝1上一点，，则根据双曲线定义，

    　　(1)由题设知，A，B，C三点在双曲线的同一支上，不妨设在双曲线的上支，故|AF|＝．∵|AF|，|BF|，|CF|成等差数列，∴6e＝，即＝12．

    　　(2)∵A，C在双曲线上，∴＝1，两式相减，12于是，AC的垂直平分线方程为y－6＝－，即y－6＝，它经过定点．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：导学大课堂选修数学1-1苏教版 苏教版 题型：044

    在双曲线＝－1的上支上有不同的三点A(x1，y1)、B(x2，6)、C(x3，y3)，与焦点F(0，5)的距离成等差数列．

    (1)求y1＋y3的值；

    (2)求证：线段AC的垂直平分线经过某一定点，并求出定点坐标．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    在双曲线－＝－1的一支上有不同的三点A(x1，y1)，B(x2，6)，C(x3，y3)，它们与焦点F(0，5)的距离成等差数列．

    (1)求y1＋y3；(2)求证线段AC的垂直平分线经过一定点．

    查看答案和解析>>

    科目：高中数学 来源：黄冈新内参·高考（专题）模拟测试卷·数学 题型：044

    在双曲线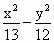＝－1的一支上有不同的三点A(，)，B(，6)，C(，)与焦点F(0，5)的距离成等差数列．

    (1)求

    (2)求证：线段AC的垂直平分线经过某一定点，并求出定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源：高考零距离　二轮冲刺优化讲练　数学 题型：044

    在双曲线－＝1的一支上有三个不同的点A(x1，y1)、B(，6)、C(x2，y2)，它们与焦点F(0，5)的距离成等差数列，求y1＋y2的值．

    查看答案和解析>>

    同步练习册答案