
分析 (1)先根据椭圆的定义得到|PF1|+|PF2|=2a,然后根据点P(x0,y0)满足0<$\frac{{{x}_{0}}^{2}}{2}$+y02<1,得出点P在椭圆内部,最后根据点P在椭圆上时|PF1|+|PF2|最大,可确定答案;
(2)直接联立直线方程和椭圆方程,化为关于x的一元二次方程后,利用判别式判断.
解答 解:(1)由题意可知|PF1|+|PF2|=2a.
点P(x0,y0)满足0<$\frac{{{x}_{0}}^{2}}{2}$+y02<1,
得出点P在椭圆内部,且与原点不重合,
∵当点P在椭圆上时|PF1|+|PF2|最大,
最大值为2a=2$\sqrt{2}$,而点P在椭圆内部,
∴|PF1|+|PF2|<2$\sqrt{2}$.
∵当点P在线段F1F2上除原点时,|PF1|+|PF2|最小,最小值为2,
∴|PF1|+|PF2|≥2.
则|PF1|+|PF2|的取值范围为[2,2$\sqrt{2}$);
(2)联立$\left\{\begin{array}{l}{\frac{{x}_{0}}{2}x+{y}_{0}y=1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得$(2{{y}_{0}}^{2}+{{x}_{0}}^{2}){x}^{2}-4{x}_{0}x+4-4{{y}_{0}}^{2}=0$.
△=$(-4{x}_{0})^{2}-4(2{{y}_{0}}^{2}+{{x}_{0}}^{2})(4-4{{y}_{0}}^{2})$=$16{{y}_{0}}^{2}({{x}_{0}}^{2}+2{{y}_{0}}^{2}-2)$.
∵0<$\frac{{{x}_{0}}^{2}}{2}$+y02<1,∴${{x}_{0}}^{2}+2{{y}_{0}}^{2}-2<0$.
则当y0=0时,△=0,直线$\frac{{x}_{0}}{2}$x+y0y=1与椭圆C有1个交点;
当y0≠0时,直线$\frac{{x}_{0}}{2}$x+y0y=1与椭圆C无交点.
点评 本题主要考查椭圆的定义、椭圆的简单性质,解答的关键是在区域的边界上利用椭圆的定义,即椭圆上点到两焦点的距离的和等于2a.对于(2)的求解,直接利用判别式法即可,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,0] | B. | [-3,0) | C. | [-3,0)∪{2} | D. | [-3,0]∪{2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x=-1,y=2} | B. | (-1,2) | C. | {-1,2} | D. | {(-1,2)} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
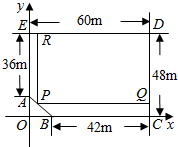 某房地产公司要在荒地ABCDE上划出一块矩形地面DRPQ建造一幢公寓.
某房地产公司要在荒地ABCDE上划出一块矩形地面DRPQ建造一幢公寓.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:1 | B. | 3:1 | C. | 9:1 | D. | 1:9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com