
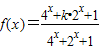 .若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是 .
.若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是 . 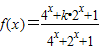 的解析式可化为f(x)=
的解析式可化为f(x)=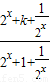 ,令t=
,令t=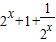 ,(t≥3),则f(x)=y=1+
,(t≥3),则f(x)=y=1+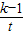 ,结合反比例函数的单调性,分类讨论函数的单调性,并分析出函数的值域,构造关于k的不等式,求出各种情况下实数k的取值范围,最后综合讨论结果,可得实数k的取值范围.
,结合反比例函数的单调性,分类讨论函数的单调性,并分析出函数的值域,构造关于k的不等式,求出各种情况下实数k的取值范围,最后综合讨论结果,可得实数k的取值范围. =
=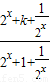
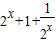 ,(t≥3)
,(t≥3)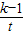
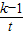 在[3,+∞)上为增函数
在[3,+∞)上为增函数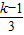 ,1)
,1)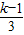 )≥1,就可以满足条件
)≥1,就可以满足条件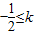 <1
<1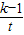 在[3,+∞)上为减函数
在[3,+∞)上为减函数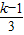 ]
]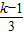 ,
,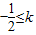 ≤4
≤4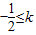 ≤4
≤4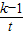 ,是解答的关键.
,是解答的关键. 

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源:2012-2013学年浙江省名校新高考研究联盟高三(上)12月联考数学试卷(理科)(解析版) 题型:填空题
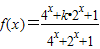 .若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是 .
.若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是 .查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都市高新区高三2月月考文科数学试卷(解析版) 题型:选择题
对于函数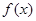 ,若存在
,若存在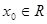 ,使
,使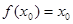 成立,则称
成立,则称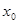 为
为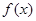 的不动点. 已知函数
的不动点. 已知函数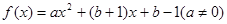 ,若对任意实数b,函数
,若对任意实数b,函数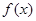 恒有两个相异的不动点,则实数
恒有两个相异的不动点,则实数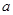 的取值范围是 ( )
的取值范围是 ( )
A.(0,1) B.(1,+∞) C.[0,1) D.以上都不对
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省六校高三联考数学理卷 题型:解答题
((本题满分13分)
已知 ,函数
,函数 .
.
(1) 若函数 在
在 上为减函数,求实数
上为减函数,求实数 的取值范围;
的取值范围;
(2) 令 ,已知函数
,已知函数 .若对任意
.若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com