（本小题满分11分）（注意：在试题卷上作答无效）
已知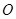
为坐标原点，向量
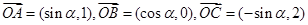，点
是直线
上的一点，且点
分有向线段
的比为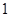
．
（1）记函数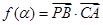
，
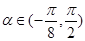，讨论函数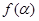
的单调性，并求其值域；
（2）若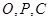
三点共线，求
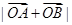的值．
（1）函数
的单调递增区间为
，单调递减区间为
，
，其值域为
；
（2）
。
【解析】(1)设P(x,y),根据点B分有向线段
的比为1，可知点B为线段AP的中点，根据中点坐标公式可求出P的坐标.进而可求出关于
的函数关系式，再求值域.
（2）根据O、P、C三点共线所以
，根据向量平行的坐标表示，可求出
的值.
由于
,由
求出
代入左边式子即可.
依题意知：
，设点
的坐标为
，则：
，所以
，点的坐标为
．．．．．．2分
（1）
，．．．．．．4分
由
可知函数的单调递增区间为，
单调递减区间为，．．．．．．6分
所以，其值域为；．．．．．．8分
（2）由
三点共线的
，．．．．．．10分
，
．．．．．．．12分
芝麻开花课程新体验系列答案科目：高中数学 来源：2013届浙江省高二下学期期中文科数学试卷（解析版） 题型：解答题
(本小题满分11分) 已知函数
，其中
．
(1) 当
时，求
的单调区间；
(2) 证明：对任意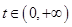
，在区间
内存在零点．
查看答案和解析>>
科目：高中数学 来源：2011-2012学年福建省高二上学期期中考试理科数学 题型：解答题
（本小题满分11分）
已知a、b、c为三角形ABC中角A、B、C的对边，且
，求这个三角形的最大内角.
查看答案和解析>>
科目：高中数学 来源：2010年陕西省西安市铁一中高二下学期期中考试数学（理） 题型：解答题
（本小题满分11分）已知，
;
（1）试由此归纳出当
时相应的不等式；
（2）试用数学归纳法证明你在第（1）小题得到的不等式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
．
的单调递增区间；
，
，求
的值．
，
或
,
．求
； （2） ( C
)
；