
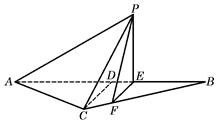
 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
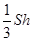 =
= 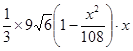 =
=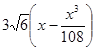 ,(0<x<3
,(0<x<3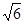 )
)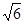
 ,又
,又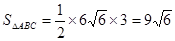 ,
,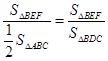 =
=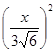 ,
,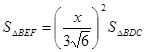 =
=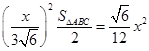 代入体积公式得
代入体积公式得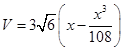 ,(0<x<3
,(0<x<3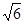 );
);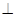 AB,那么翻折后,显然有PE
AB,那么翻折后,显然有PE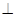 EF,又PE
EF,又PE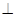 AE,
AE,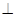 面ABC,即PE为四棱锥的高。
面ABC,即PE为四棱锥的高。
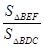 =
=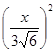 ,
,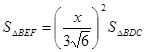 =
=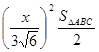 =
=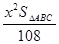 ,
,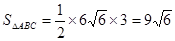
 =
=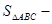
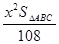 =
=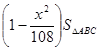 =
=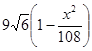
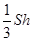 =
= 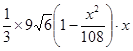 =
=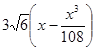 ,(0<x<3
,(0<x<3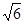 )
)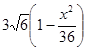 ,(0<x<3
,(0<x<3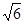 ) 令V’(x)=0得x=6
) 令V’(x)=0得x=6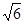 )时V’(x)><0,V(x)单调递减;
)时V’(x)><0,V(x)单调递减;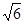


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源:不详 题型:解答题
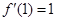 ,数列{
,数列{ }的前n项和
}的前n项和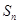 =f(n)(n∈N*).
=f(n)(n∈N*). }的通项公式;
}的通项公式;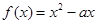
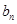 }满足
}满足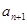 +
+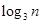 =
= 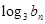 ,求数列{
,求数列{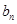 }的前n项和.
}的前n项和.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
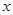 月,商品A的价格
月,商品A的价格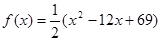 (
(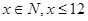 ,价格单位:元),且第
,价格单位:元),且第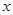 月该商品的销售量
月该商品的销售量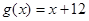 (单位:万件).(1)2011年的最低价格是多少?(2)2011年的哪一个月的销售收入最少?
(单位:万件).(1)2011年的最低价格是多少?(2)2011年的哪一个月的销售收入最少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
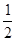 x
x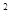 -ax+(a-1)
-ax+(a-1)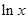 ,
,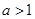 。讨论函数
。讨论函数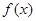 的单调性;
的单调性; 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com