
分析 (1)根据h(2)=2,h(3)=12,得到关于a,b的方程组,解出即可;
(2)求出mn的表达式,结合二次函数的性质求出mn的范围即可;
(3)问题等价于存在x使得${(\frac{b}{2})}^{x-1}$+${(\frac{c}{2})}^{x-1}$=1成立,令f(x)=${(\frac{b}{2})}^{x-1}$+${(\frac{c}{2})}^{x-1}$,根据函数的单调性求出x的范围即可.
解答 解:(1)由已知得:$\left\{\begin{array}{l}{a-b=2}\\{{a}^{2}{-b}^{2}=12}\end{array}\right.$,解得:a=4,b=2,
h(x)=f(x)-g(x)=4x-1-2x-1=${{(2}^{x-1}-\frac{1}{2})}^{2}$-$\frac{1}{4}$≤${{(2}^{2}-\frac{1}{2})}^{2}$-$\frac{1}{4}$=12,
故h(x)的最大值是12;
(2)由|h(x)|=t,|得:|2x-1-1|=t,
则m=log2(2-2t),n=log2(2+2t),
m+n=log2(2-2t)(2+2t),
0<t<$\frac{1}{2}$时,mn≤$\frac{{(m+n)}^{2}}{4}$=$\frac{{{[log}_{2}(4-{4t}^{2})]}^{2}}{4}$<1,
故0<mn<1,
综上,mn的范围是(0,1);
(3)存在x使得bx-1+cx-1=2x-1成立,
等价于存在x使得${(\frac{b}{2})}^{x-1}$+${(\frac{c}{2})}^{x-1}$=1成立,
令f(x)=${(\frac{b}{2})}^{x-1}$+${(\frac{c}{2})}^{x-1}$,
∵b<2,c<2,
则0<$\frac{b}{2}$<1,0<$\frac{c}{2}$<1,
则f(x)是减函数,
x>2,f(x)∈(0,$\frac{b+c}{2}$),
∵$\frac{b+c}{2}$>1,故必存在x0>2使得f(x0)=1,
即${(\frac{b}{2})}^{{x}_{0}-1}$+${(\frac{c}{2})}^{{x}_{0}-1}$=1,
即${b}^{{x}_{0}-1}$+${c}^{{x}_{0}-1}$=${2}^{{x}_{0}-1}$,
综上,x>2.
点评 本题考查了函数的单调性、最值问题,考查对数函数以及二次函数的性质,考查转化思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (3)(4) | C. | (2)(3) | D. | (1)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈A,2x∈B | B. | ?x∉A,2x∉B | C. | ?x∈A,2x∉B | D. | ?x∉A,2x∉B |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
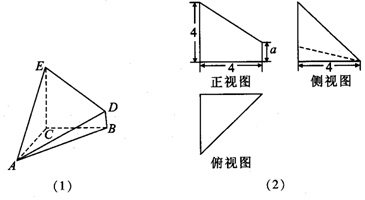
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com