
在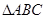 中,角
中,角 的对边分别是
的对边分别是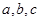 已知向量
已知向量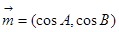
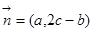 ,且
,且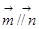 .
.
(1)求角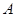 的大小;
的大小;
(2)若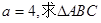 面积的最大值。
面积的最大值。
科目:高中数学 来源: 题型:解答题
如图,2012年春节,摄影爱好者S在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为 ,已知S的身高约为
,已知S的身高约为 米(将眼睛距地面的距离按
米(将眼睛距地面的距离按 米处理)
米处理)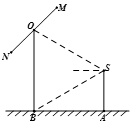
(1) 求摄影者到立柱的水平距离和立柱的高度;
(2) 立柱的顶端有一长2米的彩杆MN绕中点O在S与立柱所在的平面内旋转.摄影者有一视角范围为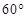 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分) 在 中,内角
中,内角 所对边的长分别为
所对边的长分别为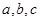 ,已知向量
,已知向量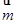 ="(1,cosA" -1),
="(1,cosA" -1),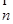 =(cosA,1)且满足
=(cosA,1)且满足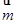 ⊥
⊥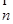 .
.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若 ,求
,求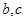 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com