
分析 (1)利用基本不等式,即可证明;
(2)利用ab+ac+bc≤a2+b2+c2即可得出.
解答 (1)证明:∵a、b均为正实数,
∴$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≥$\frac{2}{ab}$,
∵$\frac{2}{ab}$+ab$≥2\sqrt{2}$,
∴$\frac{1}{a^2}+\frac{1}{b^2}+ab≥2\sqrt{2}$(当且仅当a=b时取等号)
(2)∵(a-b)2≥0,(a-c)2≥0,(b-c)2≥0,
∴ab+ac+bc≤a2+b2+c2=4,当且仅当a=b=c时取等号.
∴ab+bc+ca的最大值是4.
点评 本题考查了基本不等式的性质,考查不等式的证明,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{x|-\frac{1}{3}<x<1\right\}$ | B. | {x|x<1} | C. | $\left\{x|x>-\frac{1}{3}\right\}$ | D. | $\left\{x|x>1或x<-\frac{1}{3}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
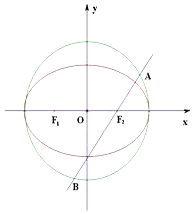 已知椭圆的标准方程为:$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{3{a}^{2}}$=1(a>0)
已知椭圆的标准方程为:$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{3{a}^{2}}$=1(a>0)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com