
分析 (Ⅰ)只要使x+2>0,4-x>0同时成立即可;
(Ⅱ)先把f(x)化为f(x)=loga(x+2)(4-x)(x∈[0,3]),再由二次函数性质及对数函数的单调性可求出f(x)的最小值,根据最小值为-2,列方程解出即可.
解答 解:(Ⅰ)由$\left\{\begin{array}{l}x+2>0\\ 4-x>0\end{array}\right.$得-2<x<4∴f(x)的定义域为(-2,4);
(Ⅱ)f(x)=loga(x+2)(4-x)(x∈[0,3])
令t=(x+2)(4-x)=-(x-1)2+9
当0≤x≤3,
∴5≤t≤9.
当0<a<1则loga9≤logat≤loga5,
∴f(x)min=loga9=-2${a^2}=\frac{1}{9}$.
又0<a<1,
∴$a=\frac{1}{3}$,
综上得$a=\frac{1}{3}$.
点评 本题考查对数函数的图象及性质,考查二次函数的最值求解,考查学生分析问题解决问题的能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2=$\frac{11}{2}$ | B. | a2=11 | C. | b2=$\frac{1}{2}$ | D. | b2=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
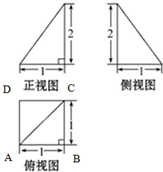 已知一四棱锥P-ABCD的三视图如图.
已知一四棱锥P-ABCD的三视图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∁U(∁UA)={A} | B. | 若A∩B=B,则A⊆B | ||
| C. | 若A={1,∅,{2}},则{2}?A | D. | 若A={1,2,3},B={x|x⊆A},则A∈B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≠0} | B. | {x|x>0} | C. | {x|x>0且x≠1} | D. | {x|x>0且x≠10} | ||||
| E. | {x|x>0且x≠1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com