
分析 对于命题p:利用指数函数的单调性可得:0<a<1.
对于命题q:函数y=lg(ax2-x+a)的定义域为R.等价于?x∈R,ax2-x+a>0.对a分类讨论,利用函数的图象与性质即可得出.如果p∨q为真命题,p∧q为假命题,则p真q假,或p假q真,即可得出.
解答 解:p:关于x的不等式ax>1(a>0,且a≠1)的解集是{x|x<0},∴0<a<1.
q:函数y=lg(ax2-x+a)的定义域为R.等价于?x∈R,ax2-x+a>0.
如果p∨q为真命题,p∧q为假命题,求实数a的取值范围.
(i)a=0 不成立.
(ii)a≠0 时,$\left\{\begin{array}{l}{a>0}\\{△=1-4{a}^{2}<0}\end{array}\right.$,解得$a>\frac{1}{2}$,即q:a$>\frac{1}{2}$.
如果p∨q为真命题,p∧q为假命题,则p真q假,或p假q真,
∴$\left\{\begin{array}{l}{0<a<1}\\{a≤\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{a≤0,或a≥1}\\{a>\frac{1}{2}}\end{array}\right.$,
解得$0<a≤\frac{1}{2}$,或a≥1.
∴实数a的取值范围是$0<a≤\frac{1}{2}$,或a≥1.
点评 本题考查了不等式的解法、简易逻辑的判定方法、函数的性质,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{19}$ | B. | $\frac{9}{23}$ | C. | $\frac{11}{23}$ | D. | $\frac{5}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
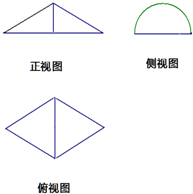 如图是某几何体的三视图,其中正视图是腰长为4的等腰三角形,侧视图是半径为2的半圆,则该几何体的表面积是( )
如图是某几何体的三视图,其中正视图是腰长为4的等腰三角形,侧视图是半径为2的半圆,则该几何体的表面积是( )| A. | $4π+4\sqrt{3}$ | B. | $8π+4\sqrt{3}$ | C. | $4π+8\sqrt{3}$ | D. | $8π+8\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
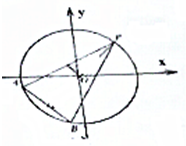 已知点P、A、B都在圆 x2+y2=r2上,其中点P的坐标是(1,1),直线PA,PB的斜率分别是k1,k2,且k1•k2=1.
已知点P、A、B都在圆 x2+y2=r2上,其中点P的坐标是(1,1),直线PA,PB的斜率分别是k1,k2,且k1•k2=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com