
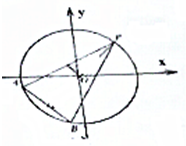
 已知点P、A、B都在圆 x2+y2=r2上,其中点P的坐标是(1,1),直线PA,PB的斜率分别是k1,k2,且k1•k2=1.
已知点P、A、B都在圆 x2+y2=r2上,其中点P的坐标是(1,1),直线PA,PB的斜率分别是k1,k2,且k1•k2=1.分析 (1)证明圆心到直线PA,PB的距离相等,即可证明结论;
(2)由(1)可得OP⊥AB,即可证明结论,
解答 证明:(1)设P的坐标是(1,1),在圆 x2+y2=r2上,∴r=$\sqrt{2}$.
∵直线PA,PB的斜率分别是k1,k2,k1•k2=1,
∴PA:y-1=k1(x-1),∴圆心到直线的距离d=$\frac{|-{k}_{1}+1|}{\sqrt{{{k}_{1}}^{2}+1}}$,
以$\frac{1}{{k}_{1}}$代入,d′=$\frac{|-{k}_{1}+1|}{\sqrt{{{k}_{1}}^{2}+1}}$,即圆心到直线PA,PB的距离相等,
∴PA=PB,
∴△PAB是等腰三角形;
(2)由(1)可得OP⊥AB,
∵kOP=1,∴直线AB的斜率为定值-1.
点评 本题考查直线与圆的位置关系,考查点到直线的距离公式,考查学生分析解决问题的能力,属于中档题.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | π | C. | -2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{6}}}{3}$ | B. | $\frac{{4\sqrt{6}}}{3}$ | C. | $\sqrt{6}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2=$\frac{11}{2}$ | B. | a2=11 | C. | b2=$\frac{1}{2}$ | D. | b2=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com