
(本题满分12分) 某企业常年生产一种出口产品,根据预测可知,进入2l世纪以来,该产品的产量平稳增长.记2008年为第1年,且前4年中,第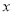 年与年产量
年与年产量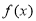 (万件)之间的关系如下表所示:
(万件)之间的关系如下表所示:
| 1 | 2 | 3 | 4 |
| 4.00 | 5.58 | 7.00 | 8.44 |
若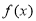 近似符合以下三种函数模型之一:
近似符合以下三种函数模型之一: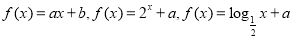 .
.
(1)找出你认为最适合的函数模型,并说明理由,然后选取08年和10年的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2014年的年产量比预计减少30%,试根据所建立的函数模型,确定2014年的年产量.
(1) ,
, ;(2)
;(2) ,
, ,2014年的实际产量为9.1万件.
,2014年的实际产量为9.1万件.
【解析】
试题分析:(1)利用待定系数法求相应模型函数的系数,即得函数模型解析式;(2)代值求解即可.
解题思路:对于函数模型应用题,要根据题中的条件合理选取函数模型,利用待定系数法进行求解.
试题解析:(1)符合条件的是 , 1分
, 1分
若模型为 ,则由
,则由 ,得
,得 ,即
,即 ,
,
此时 ,
,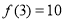 ,
, ,与已知相差太大,不符合. 3分
,与已知相差太大,不符合. 3分
若模型为 ,则
,则 是减函数,与已知不符合. 4分
是减函数,与已知不符合. 4分
由已知得 ,解得
,解得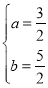 所以
所以 ,
, . 8分
. 8分
(2)2014年预计年产量为 ,, 9分
,, 9分
2014年实际年产量为 , 11分.
, 11分.
答:最适合的模型解析式为 ,
, .2014年的实际产量为9.1万件
.2014年的实际产量为9.1万件
考点:1.函数模型应用题;2.待定系数法.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源:2014-2015学年山东省泰安市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
正项等比数列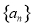 的公比为2,若
的公比为2,若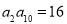 ,则
,则 的值是
的值是
A.8 B.16 C.32 D.64
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省广州市高三1月模拟理科数学试卷(解析版) 题型:选择题
一算法的程序框图如图,若输出的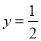 , 则输入的
, 则输入的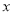 的值可能为( )
的值可能为( )
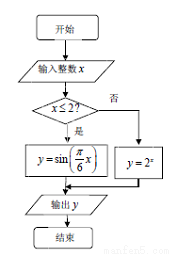
A.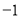 B.
B.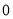 C.
C.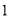 D.
D.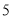
查看答案和解析>>
科目:高中数学 来源:2014-2015学年陕西宝鸡卧龙寺中学高二上学期期末命题比赛数学试卷(解析版) 题型:选择题
在下边的列联表中,类1中类B所占的比例为 ( )
Ⅱ | |||
类1 | 类2 | ||
Ⅰ | 类A | a | b |
类B | c | d | |
A.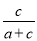 B.
B.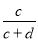 C.
C.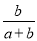 D.
D.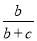
查看答案和解析>>
科目:高中数学 来源:2014-2015学年陕西宝鸡卧龙寺中学高二上学期期末命题比赛数学试卷(解析版) 题型:选择题
在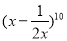 的展开式中,x4的系数为( )
的展开式中,x4的系数为( )
A.-120 B.120 C.-15 D.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com