
·ÖÎö ¶Ô|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{3}$Á½±ßƽ·½µÃ³ö$\overrightarrow{a}•\overrightarrow{b}$£¬¼ÆËã|3$\overrightarrow{a}$-2$\overrightarrow{b}$|2¼´¿ÉµÃ³ö´ð°¸£®
½â´ð ½â£º¡ß|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{3}$£¬¡à|$\overrightarrow{a}$-$\overrightarrow{b}$|2=${\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=3£¬
¼´1-2$\overrightarrow{a}•\overrightarrow{b}$+4=3£¬¡à$\overrightarrow{a}•\overrightarrow{b}$=1£®
¡à|3$\overrightarrow{a}$-2$\overrightarrow{b}$|2=9${\overrightarrow{a}}^{2}$-12$\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}$=9-12+16=13£®
¡à|3$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{13}$£®
¹Ê´ð°¸Îª£º$\sqrt{13}$£®
µãÆÀ ±¾Ì⿼²éÁËƽÃæÏòÁ¿µÄÊýÁ¿»ýÔËË㣬ÊôÓÚÖеµÌ⣮


 ÆßÐÇͼÊé¿ÚËãËÙËãÌìÌìÁ·ÏµÁдð°¸
ÆßÐÇͼÊé¿ÚËãËÙËãÌìÌìÁ·ÏµÁдð°¸ ³õÖÐѧҵ¿¼ÊÔµ¼ÓëÁ·ÏµÁдð°¸
³õÖÐѧҵ¿¼ÊÔµ¼ÓëÁ·ÏµÁдð°¸
| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | B£® | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=11 | C£® | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1 | D£® | $\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{9}$=1 |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
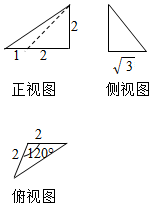 ijÈýÀâ׶µÄÈýÊÓͼÈçͼËùʾ£¬Ôò¸ÃÈýÀâ׶µÄËĸöÃæÖУ¬Ãæ»ý×î´óµÄÃæµÄÃæ»ýÊÇ£¨¡¡¡¡£©
ijÈýÀâ׶µÄÈýÊÓͼÈçͼËùʾ£¬Ôò¸ÃÈýÀâ׶µÄËĸöÃæÖУ¬Ãæ»ý×î´óµÄÃæµÄÃæ»ýÊÇ£¨¡¡¡¡£©| A£® | $4\sqrt{3}$ | B£® | $2\sqrt{3}$ | C£® | $\frac{{4\sqrt{3}}}{3}$ | D£® | $\frac{{2\sqrt{3}}}{3}$ |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | a£¾bsin A | B£® | a=bsinA | C£® | a¡ÜbsinA | D£® | a¡Ýbsin A |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | $\sqrt{3}$ | B£® | $\frac{{\sqrt{3}}}{2}$ | C£® | 1 | D£® | $\frac{1}{2}$ |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
| X | 0 | 1 | 2 | 3 |
| P | 0.1 | 0.3 | 2a | a |
²é¿´´ð°¸ºÍ½âÎö>>
¹ú¼ÊѧУÓÅÑ¡ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com