
 为坐标原点,双曲线
为坐标原点,双曲线 和椭圆
和椭圆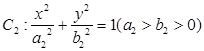 均过点
均过点 ,且以
,且以 的两个顶点和
的两个顶点和 的两个焦点为顶点的四边形是面积为2的正方形.
的两个焦点为顶点的四边形是面积为2的正方形. 的方程;
的方程; ,使得
,使得 与
与 交于
交于 两点,与
两点,与 只有一个公共点,且
只有一个公共点,且 ?证明你的结论.
?证明你的结论.
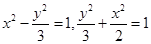 (2)不存在
(2)不存在 的两个顶点和
的两个顶点和 的两个焦点的坐标,求的
的两个焦点的坐标,求的 的值,再结合点
的值,再结合点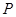 在双曲线上,代入双曲线结合
在双曲线上,代入双曲线结合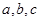 之间的关系即可求的
之间的关系即可求的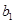 的值,得到双曲线的方程,椭圆的焦点坐标已知,点
的值,得到双曲线的方程,椭圆的焦点坐标已知,点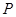 在椭圆上,利用椭圆的定义
在椭圆上,利用椭圆的定义 即为
即为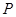 到两焦点的距离之和,求出距离即可得到
到两焦点的距离之和,求出距离即可得到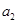 的值,利用
的值,利用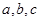 之间的关系即可求出
之间的关系即可求出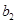 的值,得到椭圆的标准方程.
的值,得到椭圆的标准方程.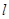 的斜率不存在时,直线
的斜率不存在时,直线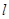 与
与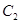 只有一个公共点,即直线经过
只有一个公共点,即直线经过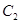 的顶点,得到直线
的顶点,得到直线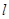 的方程,代入双曲线求的
的方程,代入双曲线求的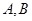 点的坐标验证是否符合等式
点的坐标验证是否符合等式 ,当直线
,当直线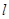 的斜率存在时,直线
的斜率存在时,直线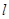 的方程为
的方程为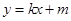 ,联立直线
,联立直线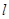 与双曲线消元得到二次方程,再利用根与系数之间的关系得到关于
与双曲线消元得到二次方程,再利用根与系数之间的关系得到关于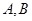 两点横纵坐标之和的表达式,利用
两点横纵坐标之和的表达式,利用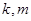 出
出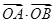 ,再立直线
,再立直线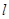 与椭圆的方程
与椭圆的方程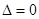 即可得到
即可得到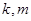 直线的关系,可得到内积
直线的关系,可得到内积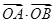 不可能等于0,进而得到
不可能等于0,进而得到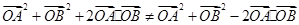 ,即
,即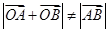 ,即不存在这样的直线.
,即不存在这样的直线. ,由题可得
,由题可得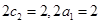 ,从而
,从而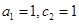 ,因为点
,因为点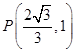 在双曲线
在双曲线 上,所以
上,所以 ,由椭圆的定义可得
,由椭圆的定义可得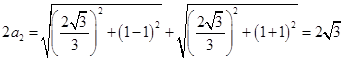
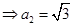 ,于是根据椭圆
,于是根据椭圆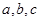 之间的关系可得
之间的关系可得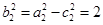 ,所以
,所以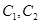 的方程为
的方程为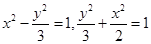 .
. 垂直于
垂直于 轴,即直线
轴,即直线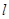 的斜率不存在,因为
的斜率不存在,因为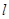 与
与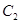 只有一个公共点,所以直线的方程为
只有一个公共点,所以直线的方程为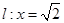 或
或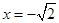 ,
,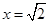 时,易知
时,易知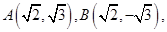 所以
所以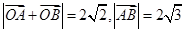 ,此时
,此时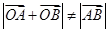 .
.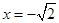 时,同理可得
时,同理可得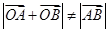 .
. 不垂直于
不垂直于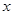 轴时,即直线
轴时,即直线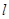 的斜率存在且设直线
的斜率存在且设直线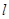 的方程为
的方程为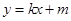 ,联立直线与双曲线方程
,联立直线与双曲线方程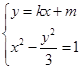 可得
可得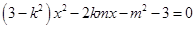 ,当
,当 与
与 相交于
相交于 两点时,设
两点时,设 ,则
,则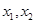 满足方程
满足方程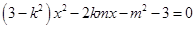 ,由根与系数的关系可得
,由根与系数的关系可得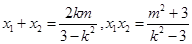 ,于是
,于是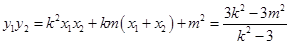 ,联立直线
,联立直线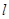 与椭圆
与椭圆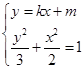 可得
可得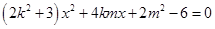 ,因为直线
,因为直线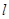 与椭圆只有一个交点,
与椭圆只有一个交点,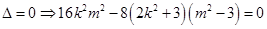 ,化简可得
,化简可得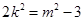 ,因此
,因此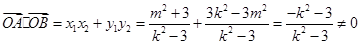 ,
,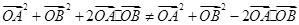 ,即
,即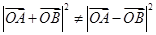 ,所以
,所以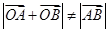 ,
, .
.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源:不详 题型:解答题
 +
+ =1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.
=1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com