
如图所示,在直角梯形
ABCD中,∠BAD=∠ADC=90°,CD=DA=a,AB=2a,SA⊥平面ABCD,且SA=a.
(1)
求证:△SAD、△SAB、△SCB、△SDC都是直角三角形;(2)
在SD上取点M,SC交平面ABM于N,求证:四边形ABNM为直角梯形.|
证明: (1)∵SA⊥平面ABCD,则SA⊥AB,SA⊥AD,SA⊥CD.∴△ SAD、△SAB是直角三角形.
∴ CD⊥SD.∴△SDC是直角三角形.连结 AC,
过 C作CG∥AD,交AB于G点,则AG=CD=a.又 AB=2a,∴BG=GC=a.∵∠BAD=90°,∴∠BGC=90°.∴ 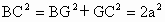 . .
在 Rt△ABC中,AB=2a,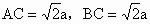 , ,
满足 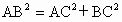 .∴AC⊥BC. .∴AC⊥BC.
又 BC⊥SA,∴BC⊥平面SAC.∴BC⊥SC,∴△ SBC是直角三角形.(2) 如图所示,∵CD∥AB,
∴ CD∥平面ABNM.
∴ MN∥AB.又 MN<AB,∴四边形ABNM是梯形.又 CD⊥平面SAD,∴MN⊥平面SAD.∴ NM⊥AM,∴四边形ABNM是直角梯形. |
(1) 证明某三角形是直角三角形,即证明直线与直线垂直,应该借助于线面垂直进行;(2)要证明某一四边形是直角梯形,必须解决如下的几个问题,一是有一组对边平行;二是有一条腰和一组对边垂直;三是这组平行边不相等. |


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
 如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在直角梯形OABC中,∠COA=∠OAB=
如图所示,在直角梯形OABC中,∠COA=∠OAB=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
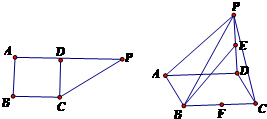 如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.
如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com