
分析 (1)根据导数的运算法则求导即可,
(2)先利用诱导公式,猜想猜想fn(x)=(x+n)sin(x+$\frac{nπ}{2}$)+(x-n)cos(x+$\frac{nπ}{2}$)(*),再根据数学归纳法证明即可.
解答 解:(1)f1(x)=f0′(x)=(sinx+cosx)+x(cosx-sinx)=(x-1)sin(-x)+(x+1)cosx,
f2(x)=f1′(x)=-sinx+(1-x)cosx+cosx-(1+x)sinx=-(2+x)sinx-(x-2)cosx,
(2)由(1)得f3(x)=f2′(x)=-(3+x)cosx+(x-3)sinx,
把f1(x),f2(x),f3(x),
f1(x)=(x+1)sin(x+$\frac{π}{2}$)+(x-1)cos(x+$\frac{π}{2}$),
f2(x)=(x+2)sin(x+$\frac{2π}{2}$)+(x-2)cos(x+$\frac{2π}{2}$),
f3(x)=(x+3)sin(x+$\frac{3π}{2}$)+(x-3)cos(x+$\frac{3π}{2}$),
猜想fn(x)=(x+n)sin(x+$\frac{nπ}{2}$)+(x-n)cos(x+$\frac{nπ}{2}$)(*),
下面用数学归纳法证明上述等式,
①当n=1时,由(1)可知,等式(*)成立,
②假设当n=k时,等式(*)成立,即fk(x)=(x+k)sin(x+$\frac{kπ}{2}$)+(x-k)cos(x+$\frac{kπ}{2}$),
则当n=k+1时,fk+1(x)=fk′(x)=sin(x+$\frac{kπ}{2}$)+(x+k)cosx+$\frac{kπ}{2}$)+cos(x+$\frac{kπ}{2}$)+(x-k)[-sin(x+$\frac{kπ}{2}$)],
=(x+k+1)cos(x+$\frac{kπ}{2}$)+[x-(k+1)][-sin(x+$\frac{kπ}{2}$)],
=(x+k+1)sin(x+$\frac{k+1}{2}$π)+[x-(k+1)]cos(x+$\frac{k+1}{2}$π),
即当n=k+1时,等式(*)成立
综上所述,当n∈N*,fn(x)=(x+n)sin(x+$\frac{nπ}{2}$)+(x-n)cos(x+$\frac{nπ}{2}$)成立.
点评 本题考查了导数的运算和诱导公式,以及数学归纳法,关键是利用诱导公式猜想出结论,属于难题.


科目:高中数学 来源:2016-2017学年重庆市高二上学期入学考试数学试卷(解析版) 题型:选择题
从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,则b>a的概率是( )
A.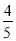 B.
B.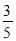 C.
C.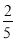 D.
D.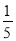
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二8月月考数学试卷(解析版) 题型:选择题
如果下边程序执行后输出的结果是990,那么在程序until后面的“条件”应为( )

A.i > 10 B.i <8 C. i <=9 D.i<9
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 抽签法 | B. | 随机数法 | C. | 系统抽样法 | D. | 分层抽样法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48 | B. | 24 | C. | 12 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com