（本题满分15分）已知直线
与曲线
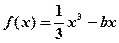相切
1）求b的值；
2）若方程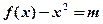
在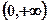
上恰有两个不等的实数根
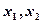，求
①m的取值范围；
②比较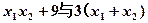
的大小
解：1）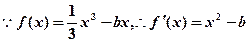
……………………………………1分
设切点位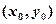
，由题意得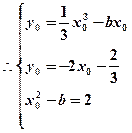
……………………………………………………………4分
联立消
，得
，由方程知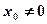
[来源:Z&xx&k.Com]
∴b=3…………………………………………………………………………5分
2)解1:设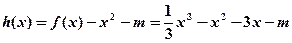
……………………6分
①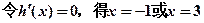
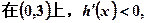故h(x
)在（0,3）上单调递减
故
h(x)在（3,
）上单调递增，……………9分
若使h(x)图象在（0,）内与x轴有两个不同的交点
则需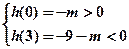
，
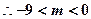……………………………………11分
此时存在
所求m的取值范围是（-9,0）……………………………………………………12分
②由①知，
满足
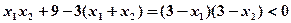
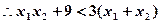…………………………………………………………15分
解析
科目：高中数学 来源： 题型：解答题
（本题14分）已知函数f （x） = ax3 +x2 -ax，其中a，x∈R．
（Ⅰ）若函数f （x）在区间（1，2）上不是单调函数，试求a的取值范围；
（Ⅱ）直接写出（不需给出运算过程）函数
的单调递减区间；
（Ⅲ）如果存在a∈（-∞，-1]，使得函数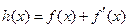
， x∈[-1, b]（b > -1），在x = -1处取得最小值，试求b的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(本小题满分13分) 已知函数
．
（Ⅰ）若函数在区间
其中a >0，上存在极
值，求实数a的取值范
围；
（Ⅱ）如果当
时，不等式
恒成立，求实数k的取值范围；
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
已知函数
的图象是连续不断的，有如下
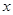、的对应填表：
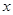| 1 | 2 | 3 | 4 | 5 | 6 |
| 123.6 | 21.5 | -7.2 | 11.7 | -53.6 | -126.9 |
在区间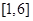
上的零点至少有（ ）个查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
是函数
的极值点．
的值； 
的单调区间；
R时，试讨论方程
的解的个数．
=_________．
的图象，只需把函数
的图象( ).
函数
在
处取得极值.
；
，如果
在开区间
上存在极小值，求实数
的取值范围.
在点x=1处连续，则a的值是 （ ）