
【题目】已知 函数f(x)=x3+(m﹣4)x2﹣3mx+(n﹣6)x∈R的图象关于原点对称,其中m,n为实常数.
(1)求m,n的值;
(2)试用单调性的定义证明:f(x)在区间[﹣2,2]上是单调函数;
(3)当﹣2≤x≤2 时,不等式f(x)≥(n﹣logma)logma恒成立,求实数a的取值范围.
【答案】
(1)解:由已知得f(x)为奇函数∴f(﹣x)=﹣f(x)即﹣x3+(m﹣4)x2+3mx+(n﹣6)=﹣x3﹣(m﹣4)x2+3mx﹣(n﹣6)恒成立,即(m﹣4)x2+(n﹣6)=0恒成立,∴m=4,n=6
(2)解:由(1)的f(x)=x3﹣12x,设﹣2≤x1<x2≤2, ![]() ,
,
∵﹣2≤x1<x2≤2,∴ ![]() ,
,
∴f(x1)﹣f(x2)>0,
即∴f(x1)>f(x2),
∴f(x)在[﹣2,2]上是减函数
(3)解:由(2)知f(x)在[﹣2,2]上是减函数,
则f(x)≥f(2)=﹣16﹣16≥(6﹣log4a)log4a,
∴(log4a﹣8)(log4a+2)≥0,
∴log4a≤﹣2或log4a≥8,
∴ ![]() 或a≥48
或a≥48
【解析】(1)利用函数的对称性,得到方程,转化求解m,n即可.(2)利用函数的单调性的定义直接证明即可.(3)利用函数的单调性结合函数的定义域,转化求解即可.


科目:高中数学 来源: 题型:
【题目】如图,一条河的两岸平行,河的宽度d=600m,一艘客船从码头A出发匀速驶往河对岸的码头B.已知|AB|=1km,水流速度为2km/h, 若客船行驶完航程所用最短时间为6分钟,则客船在静水中的速度大小为( )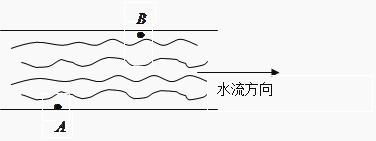
A.8km/h
B.![]() km/h
km/h
C.![]() km/h
km/h
D.10km/h
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义在R上的偶函数,对于x∈R,都有f(x+4)=f(x)+f(2)成立,当x1,x2∈[0,2]且x1≠x2时,都有![]() 给出下列四个命题:
给出下列四个命题:
①f(﹣2)=0;
②直线x=﹣4是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[4,6]上为减函数;
④函数y=f(x)在(﹣8,6]上有四个零点.
其中所有正确命题的序号为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
参考公式及数据: 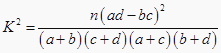
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC内接于☉O,AB=AC,直线MN切☉O于点C,弦BD∥MN,AC与BD相交于点E. 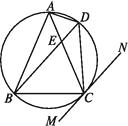
(1)求证:△ABE≌△ACD;
(2)求证:BE=BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市五一假期举行促销活动,规定一次购物不超过100元的不给优惠;超过100元而不超过300元时,按该次购物全额9折优惠;超过300元的其中300 元仍按9折优惠,超过部分按8折优惠.
(1)写出顾客购物全额与应付金额之间的函数关系,并画出流程图,要求输入购物全额,能输出应付金额.
(2)若某顾客的应付金额为282.8元,请求出他的购物全额.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com