
分析 把“?x∈[0,$\frac{π}{3}$],tanx<m”为假命题,转化为“?x∈[0,$\frac{π}{3}}$],tanx≥m”是真命题,由此求出实数m的最大值.
解答 解:“?x∈[0,$\frac{π}{3}$],tanx<m”为假命题,
可得“?x∈[0,$\frac{π}{3}}$],tanx≥m”是真命题;
又x∈[0,$\frac{π}{3}$]时,0≤tanx≤$\sqrt{3}$,
∴m≤$\sqrt{3}$,
即实数m的最大值为$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查函数最值的应用问题,也考查了全称命题与特称命题的应用问题,是基础题目.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -4 | C. | -1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
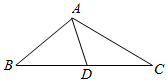 如图所示,在△ABC中,B=$\frac{π}{4}$,AC=2$\sqrt{5}$,cosC=$\frac{{2\sqrt{5}}}{5}$.
如图所示,在△ABC中,B=$\frac{π}{4}$,AC=2$\sqrt{5}$,cosC=$\frac{{2\sqrt{5}}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-$\frac{1}{2}$,$\frac{1}{2}$] | C. | [-$\frac{{\sqrt{2}}}{2}$,1] | D. | [-1,$\frac{{\sqrt{2}}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
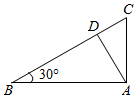 如图,在△ABC中,∠B=30°,∠BAC=90°,AD⊥BC于D.现将△ACD沿直线AD旋转一周,则在旋转过程中,直线AC与直线BD所成角的取值范围是(60°,90°).
如图,在△ABC中,∠B=30°,∠BAC=90°,AD⊥BC于D.现将△ACD沿直线AD旋转一周,则在旋转过程中,直线AC与直线BD所成角的取值范围是(60°,90°).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com