
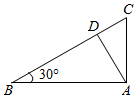
 如图,在△ABC中,∠B=30°,∠BAC=90°,AD⊥BC于D.现将△ACD沿直线AD旋转一周,则在旋转过程中,直线AC与直线BD所成角的取值范围是(60°,90°).
如图,在△ABC中,∠B=30°,∠BAC=90°,AD⊥BC于D.现将△ACD沿直线AD旋转一周,则在旋转过程中,直线AC与直线BD所成角的取值范围是(60°,90°). 分析 由题意画出图象,结合条件求出直线AC与直线BD所成角最小值,由线面垂直的判定定理求出直线AC与直线BD所成角最大值,即可得到答案.
解答 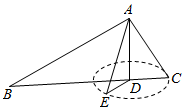 解:由题意画出图象:
解:由题意画出图象:
△ACD沿直线AD旋转一周形成一个圆锥,
底面圆的圆心是D,高是AD,
∵在△ABC中,∠B=30°,∠BAC=90°,∴∠ACB=60°,
此时直线AC与直线BD所成角最小,
当AC旋转到AE时,即DE⊥BD时,直线AC与直线BD所成角最大,
∵AD⊥圆D所在的平面,∴AD⊥BD,
∵AD∩DE=D,∴BD⊥平面ADE,则BD⊥AE,
∴直线AC与直线BD所成角最大值是90°,
即直线AC与直线BD所成角的范围是(60°,90°),
故答案为:(60°,90°).
点评 本题考查两直线所成角的取值的求法,线面垂直的判定定理,以及数形结合思想,属于中档题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com