
分析 (1)确定f(x)的解析式,分段去掉绝对值,再求最小值.(2)分别讨论f(x)在[0,1]和[1,2]上的零点个数.
解答 解:(1)由题知f(x)=x2-a|x-1|=$\left\{\begin{array}{l}{{x}^{2}-ax+a,1≤x≤2}\\{{x}^{2}+ax-a,0≤x<1}\end{array}\right.$,
当0≤x<1时,二次函数的轴为$x=-\frac{a}{2}$<0,此时f(x)在[0,1)上单调递增,
所以f(x)的最小值为m(a)=f(0)=-a;
当1≤x≤2时,二次函数的轴为$x=\frac{a}{2}>1$,
①当$\frac{a}{2}>2$即a>4时,f(x)在[1,2]上单调递减,所以f(x)的最小值为m(a)=f(2)=4-a;
②当$\frac{a}{2}≤2$即2<a≤4时,f(x)在$[1,\frac{a}{2}]上单调递减,在[\frac{a}{2},2]上单调递增$,
所以f(x)的最小值为m(a)=f($\frac{a}{2}$)=$-\frac{{a}^{2}}{4}+a$.
∴当a>4时,m(a)=-a;当2<a≤4时,m(a)=min{-a,$-\frac{{a}^{2}}{4}+a$}=-a
综上,m(a)=-a
(2)$f(x)=\left\{\begin{array}{l}{{x}^{2}+ax-a+b,0≤x≤1}\\{{x}^{2}-ax+a+b,1<x≤2}\end{array}\right.$,因为f(1)=1+b>0
①根据函数的单调性,若f(x)=0在(1,2]内没有重根,
只需$\left\{\begin{array}{l}{f(0)≤0}\\{f(1)>0}\\{f(2)≤0}\end{array}\right.$⇒$\left\{\begin{array}{l}{-a+b≤0}\\{1+b>0}\\{4-a+b≤0}\end{array}\right.$⇒$\left\{\begin{array}{l}{b≤a}\\{b>-1}\\{b≤a-4}\end{array}\right.$∴a-b≥4
②若f(x)=0在(1,2]内有重根,只需$\left\{\begin{array}{l}{f(0)≤0}\\{f(1)>0}\\{△=0}\\{1<\frac{a}{2}≤2}\end{array}\right.$⇒$\left\{\begin{array}{l}{b>-1}\\{b<a}\\{b=\frac{{a}^{2}}{4}-a}\\{2<a≤4}\end{array}\right.$
$由-1<b=\frac{{a}^{2}}{4}-a<a,得a≠2,a<8$
$a-b=a-(\frac{{a}^{2}}{4}-a)=-\frac{{a}^{2}}{4}+2a=-(\frac{a}{2}-2)^{2}+4$∈(3,4]
③当f(x)在[0,1]上没根,在[1,2]上有两个不等根,
只需$\left\{\begin{array}{l}{f(0)>0}\\{f(1)>0}\\{f(2)≥0}\\{△>0}\\{1<\frac{a}{2}≤2}\end{array}\right.$⇒$\left\{\begin{array}{l}{b-a>0}\\{b>-1}\\{a-b≤4}\\{2<a≤4}\\{{a}^{2}-4(a+b)>0}\end{array}\right.$
由线性规划
知-3<a-b≤4
综上,a-b>-3.
点评 本题考查了分段函数的最值问题,同时考查了二次函数根的分布问题,运用了分类讨论的数学思想,本题属于难题,综合性较强.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -4 | C. | -1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
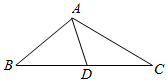 如图所示,在△ABC中,B=$\frac{π}{4}$,AC=2$\sqrt{5}$,cosC=$\frac{{2\sqrt{5}}}{5}$.
如图所示,在△ABC中,B=$\frac{π}{4}$,AC=2$\sqrt{5}$,cosC=$\frac{{2\sqrt{5}}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
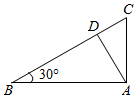 如图,在△ABC中,∠B=30°,∠BAC=90°,AD⊥BC于D.现将△ACD沿直线AD旋转一周,则在旋转过程中,直线AC与直线BD所成角的取值范围是(60°,90°).
如图,在△ABC中,∠B=30°,∠BAC=90°,AD⊥BC于D.现将△ACD沿直线AD旋转一周,则在旋转过程中,直线AC与直线BD所成角的取值范围是(60°,90°).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,2)∪(2,+∞) | B. | ($\frac{1}{2}$,+∞) | C. | (-∞,-2)∪(-2,$\frac{1}{2}$) | D. | (-∞,$\frac{1}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com