
���� ���ݶ����Լ���Ļ���˼�룬����Ŀ�е�������з������жϼ��ɣ�
��� �⣺���ڢ٣���K2�Ĺ۲�ֵk��6.635�����ڷ�����ĸ��ʲ�����0.01��ǰ���£���Ϊ�����뻼�β��й�ϵ��
�Ӷ����Լ���֪����һ�仰����˼����99%�İ�����Ϊ�����������ȷ�ģ���1%�Ŀ�������Ϊ�������ִ���
������˵��100�����̵����б���99�˻��зβ����ٴ���
���ڢڣ��Ӷ����Լ����֪�ڷ�����ĸ��ʲ�����0.01��ǰ���£���Ϊ�����뻼�β��й�ϵʱ��
�Ӷ����Լ���֪����һ�仰����˼����99%�İ�����Ϊ�����������ȷ�ģ���1%�Ŀ�������Ϊ�������ִ���
������˵ij�����̣���ô����99%�Ŀ��ܻ��зβ����ڴ���
�۴Ӷ����Լ����֪�ڷ�����ĸ��ʲ�����0.05��ǰ���£���Ϊ�����뻼�β��й�ϵʱ��
�Ӷ����Լ���֪����仰����˼����95%�İ�����Ϊ�����������ȷ�ģ���5%�Ŀ�����ʹ���ƶϴ�����ȷ��
���ϣ�����˵����ȷ���Ǣۣ�
�ʴ�Ϊ���ۣ�
���� ���⿼���˶����Լ���Ļ���˼����Ӧ�����⣬�ǻ�����Ŀ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -4 | C�� | -1 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
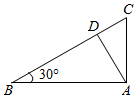 ��ͼ���ڡ�ABC�У���B=30�㣬��BAC=90�㣬AD��BC��D���ֽ���ACD��ֱ��AD��תһ�ܣ�������ת�����У�ֱ��AC��ֱ��BD���ɽǵ�ȡֵ��Χ�ǣ�60�㣬90�㣩��
��ͼ���ڡ�ABC�У���B=30�㣬��BAC=90�㣬AD��BC��D���ֽ���ACD��ֱ��AD��תһ�ܣ�������ת�����У�ֱ��AC��ֱ��BD���ɽǵ�ȡֵ��Χ�ǣ�60�㣬90�㣩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��n | B�� | m=n | ||
| C�� | m��n | D�� | m���n��С��ϵ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪f��x��=2sin��2x+$\frac{��}{3}$����
��֪f��x��=2sin��2x+$\frac{��}{3}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{1}{2}$��2���ȣ�2��+�ޣ� | B�� | ��$\frac{1}{2}$��+�ޣ� | C�� | ��-�ޣ�-2���ȣ�-2��$\frac{1}{2}$�� | D�� | ��-�ޣ�$\frac{1}{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֶ�����Ҫ���� | B�� | ��Ҫ����������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com