练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．用0、1、2、3、4这五个数字，可以组成多少个满足下列条件的没有重复数字的五位数？
    （1）奇数；
    （2）比21034大的偶数．

    分析 （1）首位不能为0，个位是奇数，问题得以解决．
    （2）需要分类讨论，当末位数字是0时，当末位数字是2时，当末位数字是4时，根据分类计数原理可得．

    解答 解：（1）先排个位，再排首位，其它任意排，可组成奇数个数为$A_2^1A_3^1A_3^3=36$个奇数；
    （2）①当末位数字是0时，首位数字可以为2或3或4，满足条件的数共有3×A33=18个．
    ②当末位数字是2时，首位数字可以为3或4，满足条件的数共有2×A33=12个．
    ③当末位数字是4时，首位数字是3的有A33=6个，首位数字是2时，有3个，共有9个．
    综上知，比21034大的偶数共有18+12+9=39个．

    点评 本题考查有限制条件问题的计数问题，要注意对特殊元素或者特殊位置进行优先考虑，注意分类加法原理和分步乘法原理的运用，考查学生的分类讨论思想．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

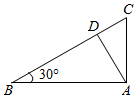    17．如图，在△ABC中，∠B=30°，∠BAC=90°，AD⊥BC于D．现将△ACD沿直线AD旋转一周，则在旋转过程中，直线AC与直线BD所成角的取值范围是（60°，90°）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知$\overrightarrow a$=（1，-2），$\overrightarrow b$=（1，λ），且$\overrightarrow a$与$\overrightarrow b$的夹角为钝角，则实数λ的取值范围是（　　）
    A．（$\frac{1}{2}$，2）∪（2，+∞）B．（$\frac{1}{2}$，+∞）C．（-∞，-2）∪（-2，$\frac{1}{2}$）D．（-∞，$\frac{1}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．“x2≥1”是“x＞1”的（　　）
    A．充分而不必要条件B．必要而不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．在矩形ABCD中，AB=4$\sqrt{5}$，AD=2$\sqrt{5}$，将△ABD沿BD折起，使得点A折起至A′，设二面角A′-BD-C的大小为θ．
    （1）当θ=90°时，求A′C的长；
    （2）当cosθ=$\frac{1}{4}$时，求BC与平面A′BD所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．求函数f（x）=-x2+4x-6，x∈[0，5]的值域（　　）
    A．[-6，-2]B．[-11，-2]C．[-11，-6]D．[-11，-1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设函数f（x）=axlnx（a≠0），若f′（e）=2，则f（e）的值为（　　）
    A．$\frac{e}{2}$B．1C．eD．2e

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．cos$\frac{9π}{4}$+tan（-$\frac{7π}{6}$）+sin21π的值为$\frac{{\sqrt{2}}}{2}-\frac{{\sqrt{3}}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．在△ABC中，角A，B，C所对的边为a，b，c．若a=2，$\frac{tanA}{tanB}$=$\frac{4}{3}$，则△ABC面积的最大值为$\frac{7}{4}$．

    查看答案和解析>>

    同步练习册答案