
分析 (1)利用诱导公式可求tanα的值,进而利用诱导公式,同角三角函数基本关系式化简所求即可计算得解.
(2)利用同角三角函数基本关系式化简所求即可计算得解.
解答 (本题满分为10分)
解:因为tan(π+α)=-$\frac{1}{2}$,可得:tanα=-$\frac{1}{2}$,…(2分)
(1)原式=$\frac{-2cosα-3(-sinα)}{4cosα+sin(-α)}$
=$\frac{-2cosα+3sinα}{4cosα-sinα}$
=$\frac{-2+3tanα}{4-tanα}$ …(4分)
=$\frac{-2+3×(-\frac{1}{2})}{4-(-\frac{1}{2})}$
=-$\frac{7}{9}$.…(5分)
(2)sin2α-2sinαcosα+4cos2α
=$\frac{si{n}^{2}α-2sinαcosα+4co{s}^{2}α}{si{n}^{2}α+co{s}^{2}α}$ …(7分)
=$\frac{ta{n}^{2}α-2tanα+4}{ta{n}^{2}α+1}$…(9分)
=$\frac{\frac{1}{4}+1+4}{\frac{1}{4}+1}$
=$\frac{21}{5}$.…(10分)
点评 本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{8π}{3}$ | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
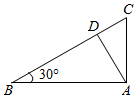 如图,在△ABC中,∠B=30°,∠BAC=90°,AD⊥BC于D.现将△ACD沿直线AD旋转一周,则在旋转过程中,直线AC与直线BD所成角的取值范围是(60°,90°).
如图,在△ABC中,∠B=30°,∠BAC=90°,AD⊥BC于D.现将△ACD沿直线AD旋转一周,则在旋转过程中,直线AC与直线BD所成角的取值范围是(60°,90°).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
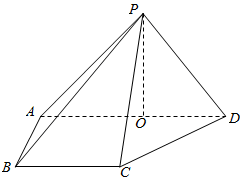 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>n | B. | m=n | ||
| C. | m<n | D. | m与的n大小关系不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com