
A.1 B.2 C.3 D.4
思路解析:本题综合考查幂的运算,指数函数性质,方程与幂的联系,①运用指数函数性质和幂的运算法则比较幂的大小;②结合幂的运算法则和函数的奇偶性的定义进行判断;③运用幂的运算法则计算进行判断;④运用换元法解出x的值进行判断.
∵8<9![]() 23<32
23<32![]() (
(![]() )6<(
)6<(![]() )6
)6![]()
![]() <
<![]() .
.
又∵![]() =
=![]() ×
×![]() =
=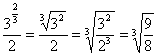 >1,
>1,
又∵3<π,∴![]() <
<![]() .
.
∴![]() <
<![]() <
<![]() <
<![]() ,因此①正确.
,因此①正确.
∵f(-x)=![]() =-f(x),
=-f(x),
∴函数f(x)= ![]() (a>0,a≠1)是奇函数.因此②也正确;
(a>0,a≠1)是奇函数.因此②也正确;
5x-1·103x=8x![]() 5x-1·53x·23x=1
5x-1·53x·23x=1![]() 54x-1=1
54x-1=1![]() 4x-1=0
4x-1=0![]() x=
x=![]() .
.
因此③也正确;
22x+4=5·2x![]() (2x)2-5·2x+4=0
(2x)2-5·2x+4=0![]() (2x-1)(2x-4)=0
(2x-1)(2x-4)=0![]() 2x=1或2x=4
2x=1或2x=4![]() x=0或x=2
x=0或x=2![]() x2+1=1或x2+1=5.
x2+1=1或x2+1=5.
因此④也是正确的.因此,选D.
答案:D


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com