
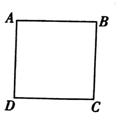
 ��ͼ��������ABCD�߳�Ϊ1����ijʱ���𣬽��߶�AB��BC��CD��DA�ֱ��Ƶ�A��B��C��D˳ʱ����ת��ͬ�ǶȦ���0������$\frac{��}{2}$��������ת��������߶���Χ�ɵķ��ͼ�����Ϊ$\frac{1}{2}$�����=��������
��ͼ��������ABCD�߳�Ϊ1����ijʱ���𣬽��߶�AB��BC��CD��DA�ֱ��Ƶ�A��B��C��D˳ʱ����ת��ͬ�ǶȦ���0������$\frac{��}{2}$��������ת��������߶���Χ�ɵķ��ͼ�����Ϊ$\frac{1}{2}$�����=��������| A�� | $\frac{��}{12}$��$\frac{5��}{12}$ | B�� | $\frac{��}{12}$��$\frac{��}{3}$ | C�� | $\frac{��}{6}$��$\frac{5��}{12}$ | D�� | $\frac{��}{6}$��$\frac{��}{3}$ |
���� ������ɵ���ת��������߶���Χ�ɵķ��ͼ��Ϊ�����Σ��߳�Ϊcos��-sin�����ã���cos��-sin����2=$\frac{1}{2}$���������cos��-sin��=��$\frac{\sqrt{2}}{2}$��cos��+sin��=$\frac{\sqrt{6}}{2}$���������cos��=$\frac{\sqrt{6}��\sqrt{2}}{4}$����������ǵ����Ǻ���ֵ���ɵý⣮
��� 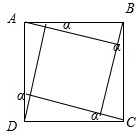 �⣺��ͼ��ʾ����ת��������߶���Χ�ɵķ��ͼ��Ϊ�����Σ�
�⣺��ͼ��ʾ����ת��������߶���Χ�ɵķ��ͼ��Ϊ�����Σ�
�߳�Ϊcos��-sin����
������ɵã���cos��-sin����2=$\frac{1}{2}$��
�ɵã�cos��-sin��=��$\frac{\sqrt{2}}{2}$�٣�2sin��cos��=$\frac{1}{2}$
��0������$\frac{��}{2}$���ɵã�cos��+sin��=$\sqrt{1+2sin��cos��}$=$\frac{\sqrt{6}}{2}$����
���ԣ��ɢ٢ڿɵã�cos��=$\frac{\sqrt{6}��\sqrt{2}}{4}$��
�ʦ�=$\frac{��}{12}$��$\frac{5��}{12}$��
��ѡ��A��
���� ������Ҫ������ͬ�����Ǻ���������ϵʽ�����Ǻ����Ķ��������Ǻ�����ֵ�е�Ӧ�ã����������ν��˼�룬����֪�õ���ת��������߶���Χ�ɵķ��ͼ���DZ߳�Ϊcos��-sin�����������ǽ���Ĺؼ��������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
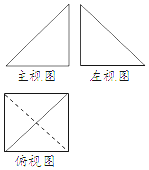 ��ͼ��ij�����������ͼ������ͼ��ȫ�ȵĵ���ֱ�������Σ�����ͼ�DZ߳�Ϊ2�������Σ���ô�������Ϊ��������
��ͼ��ij�����������ͼ������ͼ��ȫ�ȵĵ���ֱ�������Σ�����ͼ�DZ߳�Ϊ2�������Σ���ô�������Ϊ��������| A�� | $\frac{16}{3}$ | B�� | 4 | C�� | $\frac{8}{3}$ | D�� | $\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{2}$ | B�� | 2$\sqrt{5}$ | C�� | 4 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com