
 »ÁÕº£¨“—÷™∂Ø÷±œfllΩª‘≤£®x-3£©2+y2=9”⁄◊¯±Í‘≠µ„O∫Õµ„A£¨Ωª÷±œflx=6”⁄µ„B£ª
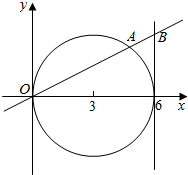
»ÁÕº£¨“—÷™∂Ø÷±œfllΩª‘≤£®x-3£©2+y2=9”⁄◊¯±Í‘≠µ„O∫Õµ„A£¨Ωª÷±œflx=6”⁄µ„B£ª∑÷Œˆ £®1£©”…“‚«Û≥ˆBµƒ◊›◊¯±Í£¨µ√µΩ÷±œflOAµƒ∑Ω≥㨔Α≤µƒ∑Ω≥ᙡ¢«Ûµ„A°¢µ„Bµƒ◊¯±Í£ª
£®2£©…Ë≥ˆOAÀ˘‘⁄÷±œfl∑Ω≥㨔Α≤µƒ∑Ω≥ᙡ¢«Û≥ˆAµƒ◊¯±Í£¨‘Ÿ«Û≥ˆBµƒ◊¯±Í£¨»ª∫Û¿˚”√œÚ¡øœ‡µ»µ√µΩπÿ”⁄Mµƒ≤Œ ˝∑Ω≥㨜˚»•≤Œ ˝∫Ûµ√¥∞∏£ª
£®3£©»°yŒ™-y£¨«˙œfl∑Ω≥Ã≤ª±‰£¨ø…µ√«˙œflCπÿ”⁄x÷·∂‘≥∆£¨‘Ÿ”…y2°›0«Ûµ√∑∂Œß£ª
£®4£©÷±Ω””…x°˙6£¨$\frac{{x}^{3}}{6-x}$°˙+°fiµ√µΩ«˙œflµƒΩ•Ω¸œfl∑Ω≥ãÆ
Ω‚¥ Ω‚£∫£®1£©”…“—÷™ø…µ√Bµ„µƒ∫·◊¯±ÍŒ™6£¨‘Ú◊›◊¯±ÍŒ™$°¿\sqrt{£®3\sqrt{5}£©^{2}-{6}^{2}}$=°¿3£¨
…Ë÷±œfllŒ™y=kx£¨∞—Bµ„◊¯±Í¥˙»Îµ√k=$°¿\frac{1}{2}$‘Ú$y=°¿\frac{1}{2}x$£¨
¡™¡¢$\left\{\begin{array}{l}{£®x-3£©^{2}+{y}^{2}=9}\\{y=°¿\frac{1}{2}x}\end{array}\right.$£¨
Ω‚µ√$\left\{\begin{array}{l}{x=\frac{24}{5}}\\{y=°¿\frac{12}{5}}\end{array}\right.$£Æ
°‡A£®$\frac{24}{5}$£¨$°¿\frac{12}{5}$£©£¨B£®6£¨°¿3£©£ª
£®2£©…ËOAÀ˘‘⁄÷±œfl∑Ω≥ÃŒ™y=kx£¨
¡™¡¢$\left\{\begin{array}{l}{y=kx}\\{£®x-3£©^{2}+{y}^{2}=9}\end{array}\right.$£¨µ√${x}_{A}=\frac{6}{{k}^{2}+1}£¨{y}_{A}=\frac{6k}{{k}^{2}+1}$£¨
”÷xB=6£¨yB=6k£¨
°‡$\overrightarrow{AB}=£®\frac{6{k}^{2}}{{k}^{2}+1}£¨\frac{6{k}^{3}}{{k}^{2}+1}£©$£¨
…ËM£®x£¨y£©£¨‘Ú$\left\{\begin{array}{l}{x=\frac{6{k}^{2}}{{k}^{2}+1}}\\{y=\frac{6{k}^{3}}{{k}^{2}+1}}\end{array}\right.$£¨œ˚»•kµ√£∫${y^2}=\frac{x^3}{6-x}$£ª
£®3£©»°yŒ™-y£¨«˙œfl∑Ω≥Ã≤ª±‰£¨°‡«˙œflCπÿ”⁄x÷·∂‘≥∆£ª
”…$\frac{{x}^{3}}{6-x}°›0$£¨Ω‚µ√£∫0°‹x£º6£¨
°‡«˙œflCµƒ∂•µ„Œ™£®0£¨0£©£ªÕº–Œ∑∂Œß¬˙◊„x° [0£¨6£©£ª
£®4£©µ±0°‹x£º6 ±£¨»Ùx°˙6£¨‘Ú$\frac{{x}^{3}}{6-x}$°˙+°fi£¨
°‡«˙œflCµƒΩ•Ω¸œfl∑Ω≥ÃŒ™x=6£Æ
µ„∆¿ ±æÂøº≤È÷±œfl∫Õ‘≤µƒŒª÷√πÿœµµƒ”¶”√£¨øº≤È¡À«˙œfl≤Œ ˝∑Ω≥õƒ«Û∑®£¨—µ¡∑¡Àº´œfiÀºœÎ∑Ω∑®µƒ”¶”√£¨ «÷–µµÃ‚£Æ


 √œΩ®∆Ω¥Ì±朵¡–¥∞∏
√œΩ®∆Ω¥Ì±朵¡–¥∞∏ ≥¨ƒ‹—ßµ‰”¶”√ÂÂø®œµ¡–¥∞∏
≥¨ƒ‹—ßµ‰”¶”√ÂÂø®œµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫Ω‚¥Ã‚
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | 1 | B£Æ | -1 | C£Æ | i | D£Æ | -i |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | 1 | B£Æ | 2 | C£Æ | 3 | D£Æ | 4 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | √¸Ã‚°∞»Ùx2=1£¨‘Úx=1°±µƒ∑Ò√¸Ã‚Œ™£∫°∞»Ùx2=1£¨‘Úx°Ÿ1°± | |
| B£Æ | √¸Ã‚°∞?x° R£¨x2+x+2£º0°±µƒ∑Ò∂® «’Ê√¸Ã‚ | |
| C£Æ | √¸Ã‚°∞»Ùx=y£¨‘Úx2=y2°±µƒƒÊ∑Ò√¸Ã‚ «ºŸ√¸Ã‚ | |
| D£Æ | “—÷™m£¨n° N£¨√¸Ã‚°∞»Ùm+n «∆Ê ˝£¨‘Úm£¨n’‚¡Ω∏ˆ ˝÷–“ª∏ˆŒ™∆Ê ˝£¨¡Ì“ª∏ˆŒ™≈º ˝°±µƒƒÊ√¸Ã‚Œ™ºŸ√¸Ã‚ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | $\frac{81¶–}{2}$ | B£Æ | $\frac{81¶–}{4}$ | C£Æ | 65¶– | D£Æ | $\frac{65¶–}{2}$ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
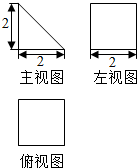
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫ÃÓø’Â
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | $\frac{7}{5}$ | B£Æ | $\frac{4}{5}$ | C£Æ | $-\frac{4}{5}$ | D£Æ | $-\frac{7}{5}$ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | £®2£¨2£© | B£Æ | £®-1£¨1£© | C£Æ | £®2£¨1£© | D£Æ | £®-4£¨-2£© |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com