
设函数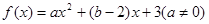 ,
,
(1)若不等式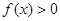 的解集
的解集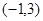 .求
.求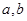 的值;
的值;
(2)若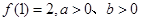 求
求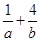 的最小值.
的最小值.
科目:高中数学 来源: 题型:解答题
某公司欲建连成片的网球场数座,用288万元购买土地20000平方米,每座球场的建筑面积为1000平方米,球场每平方米的平均建筑费用与所建的球场数有关,当该球场建n座时,每平方米的平均建筑费用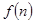 表示,且
表示,且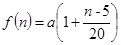 (其中
(其中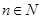 ),又知建5座球场时,每平方米的平均建筑费用为400元.
),又知建5座球场时,每平方米的平均建筑费用为400元.
(1)为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应建几座网球场?
(2)若球场每平方米的综合费用不超过820元,最多建几座网球场?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com