
分析 (Ⅰ)证明kAC•kBC=-1,即可判定三角形ABC形状;
(Ⅱ)设出直线的方程,代入A的坐标,即可求过点A且在x轴和在y轴上截距互为倒数的直线方程;
(Ⅲ)分类讨论,利用点C到直线l的距离为2,求直线l的方程.
解答 解:(Ⅰ)kAC=-1,kBC=1…(1分)kAC•kBC=-1,所以三角形ABC为直角三角形.…(3分)
(Ⅱ)设所求直线方程为$\frac{x}{a}+ay=1\;(a≠0)$,
则$\frac{-1}{a}+2a=1$即$a=-\frac{1}{2}$或a=1,
所以$-2x-\frac{1}{2}y=1$或x+y=1,
即得所求直线方程为4x+y+2=0或x+y-1=0.…(6分)
(Ⅲ)①当直线l的斜率不存在时l的方程为x=-1,此时点C到直线的距离为2,符合题意.(7分)
②当直线l的斜率存在时,设斜率为k,则直线l的方程为y-2=k(x+1),
即kx-y+k+2=0,
所以点C到直线的距离$d=\frac{{|{2k+2}|}}{{\sqrt{{k^2}+1}}}=2$,k=0,
所以直线l的方程为y-2=0.…(9分)
综上可知,直线l的方程为x+1=0和y-2=0.…(10分)
点评 本题考查直线方程,考查点到直线距离公式的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | “x=2时,x2-3x+2=0”的否命题 | |
| B. | “若α=β,则sinα=sinβ”的逆命题 | |
| C. | 平面α⊥平面α,平面γ⊥平面β,则平面α∥平面γ | |
| D. | “相似三角形的对应角相等”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
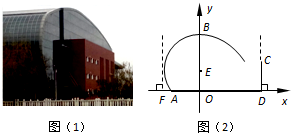 某地拟模仿图(1)建造一座大型体育馆,其设计方案侧面的外轮廓线如图(2)所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)曲线BC是抛物线y=-ax2+30(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.
某地拟模仿图(1)建造一座大型体育馆,其设计方案侧面的外轮廓线如图(2)所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)曲线BC是抛物线y=-ax2+30(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}+2$ | B. | 1 | C. | 3 | D. | $\frac{\sqrt{3}}{2}+2$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com