
| A. | “x=2时,x2-3x+2=0”的否命题 | |
| B. | “若α=β,则sinα=sinβ”的逆命题 | |
| C. | 平面α⊥平面α,平面γ⊥平面β,则平面α∥平面γ | |
| D. | “相似三角形的对应角相等”的逆否命题 |
分析 写出原命题的否命题并判断真假判断A;写出原命题的逆命题并判断真假判断B;由面面垂直的性质判断C;由互为逆否命题的两个命题共真假判断D.
解答 解:“x=2时,x2-3x+2=0”的否命题为:“x≠2时,x2-3x+2≠0”,是假命题,如x=1≠2,此时x2-3x+2=0;
“若α=β,则sinα=sinβ”的逆命题为:“若sinα=sinβ,则α=β”,是假命题,如sin$\frac{π}{6}=sin\frac{5π}{6}$,但$\frac{π}{6}≠\frac{5π}{6}$;
平面α⊥平面β,平面γ⊥平面β,则平面α∥平面γ,是假命题,原因是垂直于同一平面的两个平面平行或相交;
∵“相似三角形的对应角相等”是真命题,∴其逆否命题为真命题.
故选:D.
点评 本题考查命题的真假判断与应用,考查了命题的逆命题、否命题和逆否命题的真假判断,是基础题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 0.146 2 | B. | 0.153 8 | C. | 0.996 2 | D. | 0.853 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
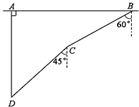 如图,在一次军事演习中,蓝方在一条东西走向公路上的A处朝正南方撤退,红方在公路B处沿南偏西60°方向实施拦截,红方行驶1000米到C处,发现前方无法通行,决定调整方向再朝南偏西45°方向前进了相同的距离,刚好在D处拦截到蓝方,求拦截点D到公路的距离.
如图,在一次军事演习中,蓝方在一条东西走向公路上的A处朝正南方撤退,红方在公路B处沿南偏西60°方向实施拦截,红方行驶1000米到C处,发现前方无法通行,决定调整方向再朝南偏西45°方向前进了相同的距离,刚好在D处拦截到蓝方,求拦截点D到公路的距离.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0” | |
| B. | 命题“若x=0,则x2-x=0”逆否命题为真命题 | |
| C. | 若命题P:?n∈N,n2>2n,则¬P:?n∈N,n2≤2n | |
| D. | 若“p∧q”为假命题,则“p∨q”为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com